
在掌握一元一次不等式、一元二次不等式、简单的高次不等式、分式不等式的解法的基础上,掌握某些简单的不等式的解法.
|

|
版权所有:()
版权所有:()
(四)巩固练习:
1.(《高考 计划》考点18“智能训练第5题”)甲、乙两人沿同一方向去
计划》考点18“智能训练第5题”)甲、乙两人沿同一方向去 地,途中都使用两种不同的速度
地,途中都使用两种不同的速度 .甲一半路程使用速度
.甲一半路程使用速度 ,另一半路程使用速度
,另一半路程使用速度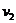 ,乙一半时间使用速度
,乙一半时间使用速度 ,另一半时间使用速度
,另一半时间使用速度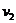 ,甲、乙两人从
,甲、乙两人从 地到
地到 地的路程与时间的函数图象及关系,有下面图中
地的路程与时间的函数图象及关系,有下面图中 个不同的图示分析(其中横轴
个不同的图示分析(其中横轴 表示时间,纵轴
表示时间,纵轴 表示路程),其中正确的图示分析为(
表示路程),其中正确的图示分析为(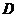 ).
).




 (1)
(1) 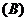 (3)
(3)  (1)或(4)
(1)或(4)
 (1)或(2)
(1)或(2)
(1) (2) (3) (4)
2.投寄本埠平信,每封信不超过 时付邮费
时付邮费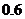 元,超过
元,超过 不超过
不超过 时付邮费
时付邮费 元,依此类推,每增加
元,依此类推,每增加 需增加邮费
需增加邮费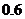 元(重量在
元(重量在 以内),如果某人投一封重量为
以内),如果某人投一封重量为 的信,他应付邮费 (
的信,他应付邮费 ( 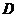 )
)

 元
元 
 元
元 
 元
元 
 元
元
(三)例题分析:
 例1.从盛满
例1.从盛满 升纯酒精的容器里倒出
升纯酒精的容器里倒出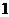 升,然后用水填满,再倒出
升,然后用水填满,再倒出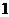 升混合溶液又用水填满,这样继续下去,如果倒第
升混合溶液又用水填满,这样继续下去,如果倒第 次时共倒出纯酒精
次时共倒出纯酒精 升,倒第
升,倒第 次时共倒出纯酒精
次时共倒出纯酒精 升,
升,
则 的表达式是
的表达式是 .
.
例2.(《高考 计划》考点18“智能训练第7题”)
某工厂八年来某种产品总产量
计划》考点18“智能训练第7题”)
某工厂八年来某种产品总产量 与时间
与时间 (年)的函数关系如右图,下列四种说法①前三年中,产量的增长的速度越来越快,②前三年中,产量的增长的速度越来越慢,③第三年后,这种产品停止生产,④第三年后,年产量保持不变,其中说法正确的是
(年)的函数关系如右图,下列四种说法①前三年中,产量的增长的速度越来越快,②前三年中,产量的增长的速度越来越慢,③第三年后,这种产品停止生产,④第三年后,年产量保持不变,其中说法正确的是
 ②与③
②与③  ②与④
②与④  ①与③
①与③  ①与④
①与④
例3.假设国家收购某种农产品的价格是 元/
元/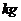 ,其中征税标准为每
,其中征税标准为每 元征
元征 元(叫做税率为
元(叫做税率为 个百分点,即
个百分点,即 ),计划可收购
),计划可收购 .为了减轻农民负担,决定税率降低
.为了减轻农民负担,决定税率降低 个百分点,预计收购可增加
个百分点,预计收购可增加 个百分点.(1)写出税收
个百分点.(1)写出税收 (元)与
(元)与 的函数关系;(2)要使此项税收在税率调节后不低于原计划的
的函数关系;(2)要使此项税收在税率调节后不低于原计划的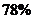 ,确定
,确定 的取值范围.
的取值范围.
解:(1)由题知,调节后税率为 ,预计可收购
,预计可收购 ,总金额为
,总金额为 元
元
∴ .
.
(2)∵元计划税收 元,
元,
∴ ,
,
得 ,
,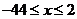 ,又∵
,又∵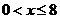 ,
,
∴ 的取值范围为
的取值范围为 .
.
例4.某航天有限公司试制一种仅由金属 和金属
和金属 合成的合金,现已试制出这种合金
合成的合金,现已试制出这种合金 克,它的体积
克,它的体积 立方厘米,已知金属
立方厘米,已知金属 的比重
的比重 小于每立方厘米
小于每立方厘米 克,大于每立方厘米
克,大于每立方厘米 克;金属
克;金属 的比重约为每立方厘米
的比重约为每立方厘米 克.
克.
(1)试用 分别表示出此合金中金属
分别表示出此合金中金属 、金属
、金属 克数的函数关系式;
克数的函数关系式;
(2)求已试制的合金中金属 、金属
、金属 克数的取值范围.
克数的取值范围.
解:(1)此合金中含 金属
金属 克、
克、 金属
金属 克, 则
克, 则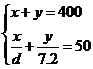 ,
,
解得 ,
, .
.
(2)∵ 在
在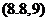 上是减函数,∴
上是减函数,∴ .
.
 在
在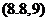 上是增函数,
上是增函数,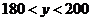 .
.
例5.(《高考 计划》考点18例3)用水清洗一堆蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用一个单位的水可清除蔬菜上残留的农药量的
计划》考点18例3)用水清洗一堆蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用一个单位的水可清除蔬菜上残留的农药量的 ,用水越多洗掉的农药量越多,但总还有农药残留在蔬菜上,设用
,用水越多洗掉的农药量越多,但总还有农药残留在蔬菜上,设用 单位量的水清洗一次后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数
单位量的水清洗一次后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数 .(1)试规定
.(1)试规定 的值,并解释其实际意义;(2)根据假定写出函数
的值,并解释其实际意义;(2)根据假定写出函数 应满足的条件和具有的性质;(3)设
应满足的条件和具有的性质;(3)设 ,现有
,现有 单位量的水,可清洗一次,也可以把水平均分成两份后清洗两次,哪种方案清洗后蔬菜上残留的农药量比较少?说明理由.
单位量的水,可清洗一次,也可以把水平均分成两份后清洗两次,哪种方案清洗后蔬菜上残留的农药量比较少?说明理由.
解答见《高考 计划》第95页.
计划》第95页.
(二)主要方法:解数学应用题的一般步骤为:(1)审题;(2)建模;(3)求解;(4)作答.
(一)主要知识:函数的综合问题主要有如下几个方面:
1.函数的概念、性质和方法的综合问题;
2.函数与其它知识,如方程、不等式、数列的综合问题;
3.函数与解析几何的综合问题;
4.联系生活实际和生产实际的应用问题.
16.下面一段话划线的部分在表述上有多处语病,请找出来任意三处并加以修改。(6分)
最高人民法院有关负责人介绍,①行政诉讼法施行以来,②人民法院依法审理、受理了大量行政案件,有效地化解了行政争议,维护了人民群众的合法权益,促进了行政机关依法行政,③行政审判的特殊职能作用日益彰显。但是,④最高人民法院开通的民意沟通信箱征集的意见来看,行政诉讼“告状难”现象依然存在。最高人民法院为此进行了深入调研,⑤并在此基础上出台了《关于保护行政诉讼当事人诉权的意见》,⑥其目的是为了督促各级人民法院进一步重视和加强行政案件受理,依法保护当事人诉讼权利,⑦切实解决行政诉讼“告状难”。
|
序号 |
修改意见 |
|
|
|
|
|
|
|
|
|
|
|
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com