
1.2010年上海世博会的主题是“城市,让生活更美好”。下列叙述中不正确的是
A.世博会前期,处理废水时加入明矾可作为混凝剂以吸附水中的杂质
B.世博会期间,利用可降解的“玉米塑料”替代一次性饭盒,可防止产生白色污染
C.世博会中国馆--“东方之冠”使用的钢筋混凝土属于高分子化合物
D.世博停车场安装催化光解设施,可将汽车尾气中CO和NOx反应生成无毒气体
22.(本小题满分12分)
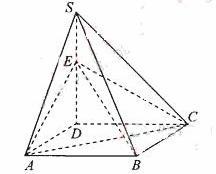 如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=
如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=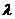 a(0<
a(0<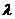 ≦1).
≦1).
(Ⅰ)求证:对任意的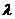
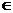 (0、1),都有AC⊥BE:
(0、1),都有AC⊥BE:
(Ⅱ)若二面角C-AE-D的大小为600C,求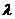 的值。
的值。
21.(本小题满分12分)
如图,正方形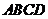 所在平面与平面四边形
所在平面与平面四边形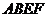 所在平面互相垂直,△
所在平面互相垂直,△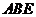 是等腰直角三角形,
是等腰直角三角形,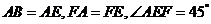
(I)求证: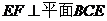 ;
;
(II)设线段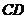 、
、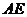 的中点分别为
的中点分别为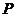 、
、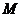 ,求证:
,求证: 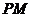 ∥
∥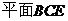
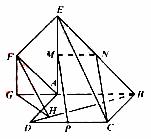 (III)求二面角
(III)求二面角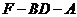 的大小。
的大小。
20.(本小题满分12分)
 如图,在四棱锥
如图,在四棱锥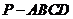 中,底面
中,底面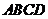 是矩形,
是矩形,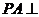 平面
平面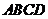 ,
,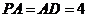 ,
,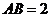 .以
.以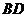 的中点
的中点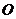 为球心、
为球心、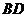 为直径的球面交
为直径的球面交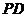 于点
于点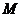 .
.
(1)求证:平面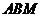 ⊥平面
⊥平面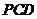 ;
;
(2)求直线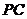 与平面
与平面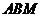 所成的角;
所成的角;
(3)求点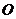 到平面
到平面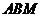 的距离.
的距离.
19.(本小题共14分)
如图,在三棱锥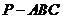 中,
中,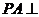 底面
底面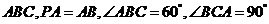 ,
,
 点
点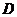 ,
,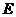 分别在棱
分别在棱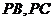 上,且
上,且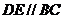
(Ⅰ)求证: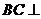 平面
平面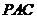 ;
;
(Ⅱ)当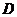 为
为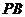 的中点时,求
的中点时,求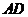 与平面
与平面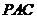 所成的角的大小;
所成的角的大小;
(Ⅲ)是否存在点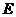 使得二面角
使得二面角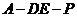 为直二面角?并说明理由.
为直二面角?并说明理由.
18.(本小题共14分)
如图,四棱锥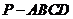 的底面是正方形,
的底面是正方形,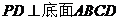 ,点E在棱PB上.
,点E在棱PB上.
 (Ⅰ)求证:平面
(Ⅰ)求证:平面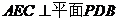 ;
;
(Ⅱ)当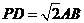 且E为PB的中点时,求AE与平面PDB所成的角的大小.
且E为PB的中点时,求AE与平面PDB所成的角的大小.
17.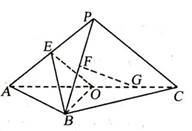 (本题满分12分)如图,平面
(本题满分12分)如图,平面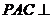 平面
平面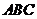 ,
,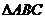
是以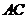 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,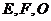 分别为
分别为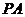 ,
,
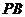 ,
,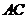 的中点,
的中点,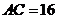 ,
,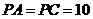 .
.
(I)设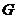 是
是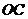 的中点,证明:
的中点,证明: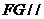 平面
平面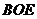 ;
;
(II)证明:在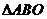 内存在一点
内存在一点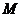 ,使
,使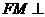 平面
平面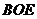 ,并求点
,并求点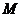 到
到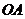 ,
,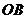 的距离.
的距离.
16.已知三个球的半径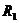 ,
,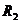 ,
,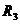 满足
满足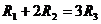 ,则它们的表面积
,则它们的表面积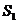 ,
,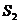 ,
,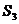 ,满足的等量关系是___________.
,满足的等量关系是___________.
15.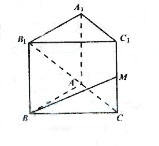 如图,已知正三棱柱
如图,已知正三棱柱 的各条棱长都相等,
的各条棱长都相等,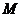 是侧 棱
是侧 棱 的中点,则异面直线
的中点,则异面直线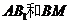 所成的角的大小是
。
所成的角的大小是
。
14.在空间直角坐标系中,已知点A(1,0,2),B(1,-3,1),点M在y轴上,且M到A与到B的距离相等,则M的坐标是________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com