
4. (2006年江苏卷)设a、b、c是互不相等的正数,则下列等式中不恒成立的是( )
A. 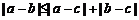 B.
B.
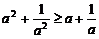
C. 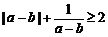 D.
D.
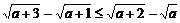
3. (2006年上海春卷)若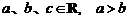 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A. 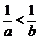 . B.
. B.
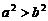 . C.
. C.
 . D.
. D. 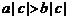 .
.
2. (2006年江西卷)若不等式x2+ax+1³0对于一切xÎ(0,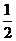 )成立,则a的取值范围是( )
)成立,则a的取值范围是( )
A. 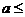 0 B.
0 B.
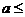 –2
C.
–2
C.
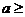 -3
D.
-3
D.
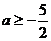
1、(上海理13)已知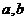 为非零实数,且
为非零实数,且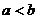 ,则下列命题成立的是 ( )
,则下列命题成立的是 ( )
A. 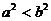 B.
B.
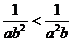 C.
C.
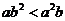 D.
D.
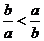
(九)不等式与导数,向量,数列的综合题
例9. 设平面上的动向量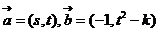 ,其中
,其中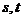 为不同时为0的两个实数,实数
为不同时为0的两个实数,实数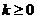 ,满足
,满足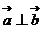
(1)求函数关系式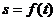 ;
;
(2)若函数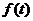 在
在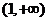 上单调递增,求
上单调递增,求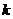 的范围;
的范围;
(3)对上述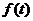 ,当
,当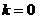 时,存在正项数列
时,存在正项数列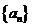 满足
满足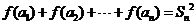 ,其中
,其中 ,证明:
,证明: 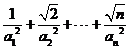 <3
<3
解:(1)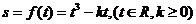
(2) 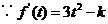 ,∴
,∴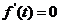 时
时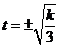
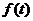 的递增区间为
的递增区间为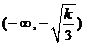 和
和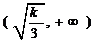
又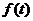 在
在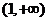 递增
递增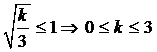
(3)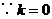 时
时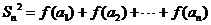
∴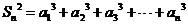
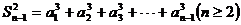
∴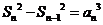
又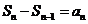 ,∴
,∴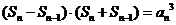
∴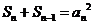
又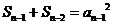 ,两式相减得
,两式相减得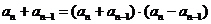
又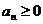 ,∴
,∴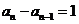
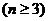
又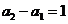 ,∴
,∴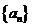 等差且公差为1,首项为1,∴
等差且公差为1,首项为1,∴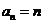
又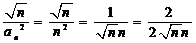
∴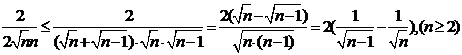
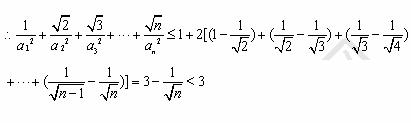
[模拟试题](答题时间:45分钟)
(八)不等式与数列、几何的综合
例8. 数列{an}的前n项和Sn=na+(n─1)nb,(n=1,2,…),a,b是常数,且b≠0,
①求证{an}是等差数列;
②求证以(an,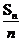 )为坐标的点Pn都落在同一直线上,并求出直线方程;
)为坐标的点Pn都落在同一直线上,并求出直线方程;
③设a=1,b=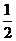 ,C是以(r,r)为圆心,r为半径的圆(r>0),求使得点P1,P2,P3都落在圆外的r 的取值范围
,C是以(r,r)为圆心,r为半径的圆(r>0),求使得点P1,P2,P3都落在圆外的r 的取值范围
证明:①根据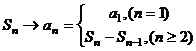 得an=a+(n─1)´ 2b,
得an=a+(n─1)´ 2b,
∴{an}是等差数列,首项为a,公比为2b
②由x=an=a+(n─1)´2b, y=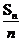 =a+(n─1)b
=a+(n─1)b
两式中消去n,得:x─2y+a─2=0,(另外算斜率也是一种办法)
(3)P1(1,0),P2(2,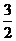 ),P3(3,2),它们都落在圆外的条件是:
),P3(3,2),它们都落在圆外的条件是:
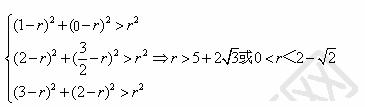
∴ r的取值范围是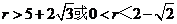
(七)不等式在函数应用题中的应用
例7. 经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度v(千米/小时)之间的关系为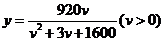 。
。
(1)在该时段内,当汽车的平均速度为多少时,车流量最大?最大车流量为多少?(精确到0.1)
(2)若要求在该时段内车流超过10千辆/小时,则汽车的平均速度应在什么范围?
解:(1)依题意,
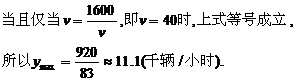
当v=40千米/小时,车流量最大,最大车流量约为11.1千辆/小时.
(2)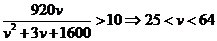
(六)含参数不等式中的参数的取值范围问题
例6. 已知关于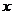 的方程
的方程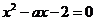 的两根为
的两根为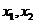 ,问:是否存在实数
,问:是否存在实数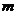 ,使得不等式
,使得不等式 对任意实数
对任意实数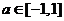 及
及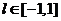 恒成立?若存在,求
恒成立?若存在,求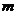 的范围,若不存在,说明理由
的范围,若不存在,说明理由
答案:存在。
(五)不等式与函数的综合
例5. 已知函数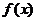 是定义在
是定义在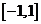 上的奇函数,若对于任意
上的奇函数,若对于任意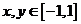 ,都有
,都有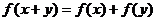 且
且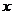 >0时,有
>0时,有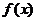 >0
>0
(1)用单调性的定义证明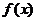 在
在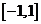 上为单调递增函数;
上为单调递增函数;
(2)解不等式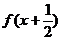 <
<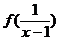 ;
;
(3)设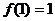 ,若
,若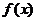 <
<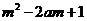 ,对所有
,对所有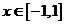 ,
,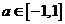 恒成立,求实数
恒成立,求实数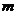 的取值范围.
的取值范围.
解:(1)证明略
(2)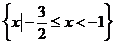
(3)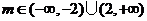
(四)不等式与命题的综合
例4. (北京文15)(本小题共12分)
记关于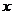 的不等式
的不等式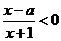 的解集为
的解集为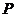 ,不等式
,不等式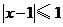 的解集为
的解集为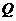 .
.
(I)若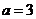 ,求
,求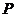 ;
;
(II)若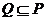 ,求正数
,求正数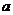 的取值范围.
的取值范围.
解:(I)由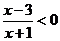 ,得
,得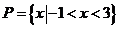 .
.
(II)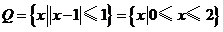 .
.
由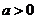 ,得
,得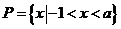 ,又
,又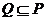 ,所以
,所以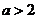 ,
,
即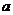 的取值范围是
的取值范围是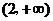 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com