
6.将函数y=sinx的图象向左平移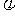
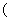 0
0 
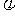 <2
<2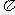
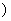 的单位后,得到函数y=sin
的单位后,得到函数y=sin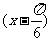 的图象,则
的图象,则 等于
( )
等于
( )
A.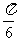 B.
B.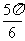 C.
C. 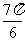 D.
D.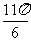
5. 已知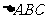 中,
中,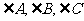 的对边分别为
的对边分别为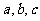 若
若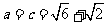 且
且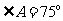 ,则
,则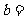 ( )
( )
A.2
B.4+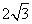 C.4-
C.4-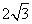 D.
D.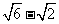
4.若将函数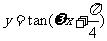
 的图象向右平移
的图象向右平移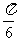 个单位长度后,与函数
个单位长度后,与函数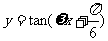 的图象重合,则
的图象重合,则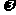 的最小值为( )
的最小值为( )
(A)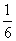 (B)
(B)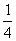 (C)
(C)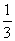 (D)
(D)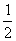 21世纪教育网
21世纪教育网
3. “sin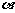 =
=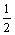 ”是“
”是“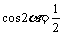 ”
” 的( )
的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
2.有四个关于三角函数的命题:
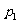 :
: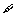 x
x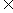 R,
R, 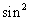
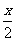 +
+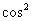
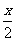 =
=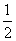 ;
; 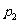 :
: 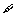 x、y
x、y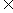 R, sin(x-y)=sinx-siny;
R, sin(x-y)=sinx-siny;
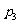 :
: 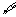 x
x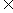
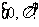 ,
, =sinx;
=sinx; 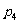 : sinx=cosy
: sinx=cosy x+y=
x+y=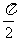 .
.
其中假命题的是( )
A.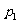 ,
,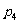 B.
B.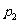 ,
,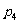 C.
C.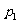 ,
,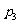 D.
D.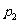 ,
,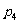
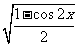
1.函数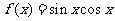 最小值是( )
最小值是( )
A.-1
B. 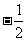 C.
C.
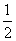 D.1
D.1
5.三角函数与简易逻辑的综合
高考对于简易逻辑的考查,总是与各部分知识综合在一起,达到考查基础知识的同时也考查简易逻辑的目的.而通过该类综合题考查三角函数部分的基本概念、性质和运算是历年来的热点.
例8.
“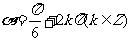 ”是“
”是“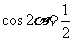 ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
答案:A
解析:当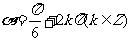 时,
时,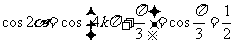 ,
,
反之,当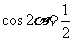 时,有
时,有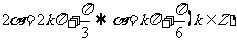 ,
,
或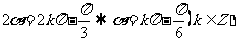 ,故应选A.
,故应选A.
点评:本题主要综合考查三角函数的基本概念、简易逻辑中充要条件的判断. 属于基础知识、基本运算的考查.
[思想方法]
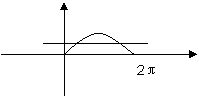
[例1]在同一平面直角坐标系中,函数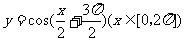 的图象和直线
的图象和直线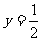 的交点个数是( )
的交点个数是( )
 A.0 B.1
C.2
D.4
A.0 B.1
C.2
D.4
解析:原函数可化为:
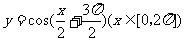 =
=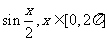 .
.
作出原函数图象,截取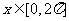 部分,其与直线
部分,其与直线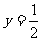 的交点个数是2个.
的交点个数是2个.
[分析]该题是数形结合思想的体现,本小题主要考查三角函数图象的性质问题,学会五点法画图,取特殊角的三角函数值画图.掌握三角函数的周期等性质是准确作图的关键.
[例2]已知向量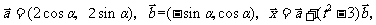
 ,且
,且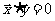 ,
,
(1)求函数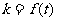 的表达式;
的表达式;
(2)若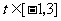 ,求
,求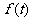 的最大值与最小值.
的最大值与最小值.
解析:(1)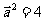 ,
,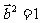 ,
,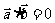 ,又
,又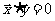 ,
,
所以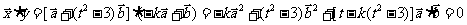 ,
,
所以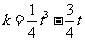 ,即
,即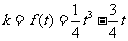 ;
;
(2)由(1)可得,令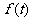 导数
导数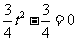 ,解得
,解得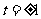 ,列表如下:
,列表如下:
|
t |
-1 |
(-1,1) |
1 |
(1,3) |
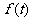 导数 导数 |
0 |
- |
0 |
+ |
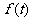 |
极大值 |
递减 |
极小值 |
递增 |
而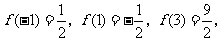 所以
所以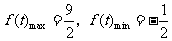 .
.
[分析]本题以三角函数和平面向量为载体,将三角函数与平面向量、导数等综合考察,体现了知识之间的融会贯通.考查了方程和函数思想,高考命题对思想方法的考查越来越得到重视.
[例3]已知函数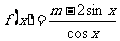 在区间
在区间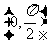 上单调递减,试求实数
上单调递减,试求实数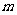 的取值范围.
的取值范围.
解析:任取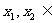
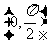 ,且
,且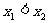 ,则不等式
,则不等式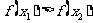 恒成立,即:
恒成立,即:
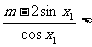
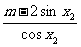 恒成立.化简得
恒成立.化简得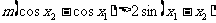 ,
,
由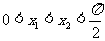 ,可知:
,可知: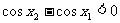 ,所以
,所以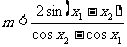 .
.
上式恒成立的条件为: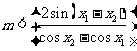 在区间
在区间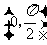 上的最小值.
上的最小值.
由于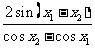
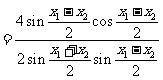
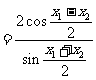
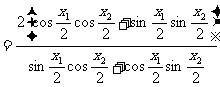
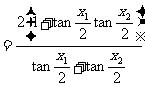 .
.
且当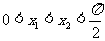 时,
时,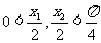 ,所以
,所以
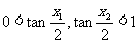 ,
,
从而
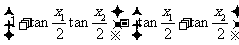
 ,
,
有  ,故
,故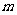 的取值范围为
的取值范围为 .
.
[分析]该题考查了转化与化归思想,根据已知条件,该题实际上是一个给出了在区间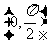 上恒成立的不等式.
上恒成立的不等式.
[专题演练]
4.三角函数与幂、指、对函数的综合
三角函数作为基本初等函数之一,具有函数的基本性质,如奇偶性、单调性、周期性,遵循复合函数图象的单调性规律,考题有时将三角函数与幂、指、对函数等结合构造复合函数研究其图象的性质也是命题的一个方向.
例7.函数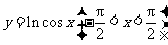 的图象是( )
的图象是( )
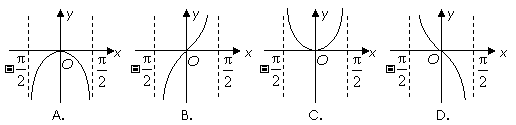

答案:A
解析: 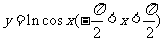 是偶函数,可排除B、D,由
是偶函数,可排除B、D,由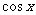 的值域可以确定.故选A.
的值域可以确定.故选A.
点评:本小题主要考查复合函数的图象识别,充分掌握偶函数的性质,余弦函数的图象及性质,另外,排除法,在复习时应引起重视,解选择题时,经常采用排除法.
3.解三角形的实际应用
对于正弦定理、余弦定理的综合考查,主要是以实际问题为载体,解决一些简单的三角形度量问题,和几何计算有关的问题.解三角形时,要灵活运用已知条件,根据正、余弦定理,列出方程,进而求解,最后还要检验是否符合题意.重点为正余弦定理及三角形面积公式,考题灵活多样,近几年经常以解答题的形式来考查,若以解决实际问题为背景的试题,有一定的难度.
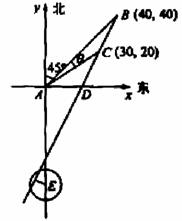 例6. 在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东
例6. 在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东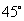 且与点A相距40
且与点A相距40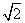 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东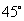 +
+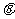 (其中sin
(其中sin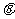 =
=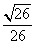 ,
,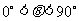 )且与点A相距10
)且与点A相距10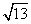 海里的位置C.
海里的位置C.
(I)求该船的行驶速度(单位:海里/小时);
(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
解析: (I)如图,AB=40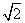 ,AC=10
,AC=10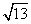 ,
,
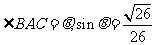 .
.
由于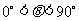 ,所以cos
,所以cos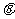 =
=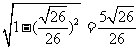 .
.
由余弦定理得BC=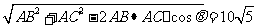 .
.
所以船的行驶速度为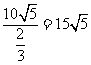 (海里/小时).
(海里/小时).
(II) 如图所示,以A为原点建立平面直角坐标系,
设点B、C的坐标分别是B(x1,y2), C(x1,y2),BC与x轴的交点为D.
由题设有,x1=y1= 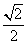 AB=40,x2=ACcos
AB=40,x2=ACcos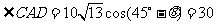 ,
,
y2=ACsin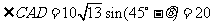 .
.
所以过点B、C的直线l的斜率k=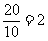 ,直线l的方程为y=2x-40.
,直线l的方程为y=2x-40.
又点E(0,-55)到直线l的距离d=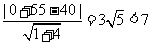 .
.
所以船会进入警戒水域.
点评:三角函数在实际问题中有很多的应用,随着课改的深入,联系实际,注重数学在实际问题的应用将分是一个热点.
2.三角函数与平面向量综合题
三角函数与平面向量是高中数学中两个活跃的“角色”,它们联手演绎了新颖度高,变化丰富的一幕幕好戏,三角函数与平面向量的综合性问题作为近年来的高考命题热点,难度不大,主要注重基础知识的考查,强调三角函数、平面向量的工具作用.从题型上看,主要包括向量与三角函数的化简、求值及证明的交汇,向量与三角函数图象、性质的交汇等.
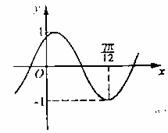 例4.将函数
例4.将函数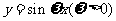 的图象按向量
的图象按向量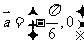 平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( ).
平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( ).
A.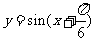 B.
B.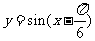
C.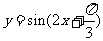 D.
D.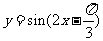
答案:C
解析:将函数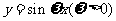 的图象按向量
的图象按向量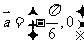 平移,即向左平移
平移,即向左平移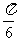 ,根据“左加右减”的平移规律,平移后的图象所对应的解析式为
,根据“左加右减”的平移规律,平移后的图象所对应的解析式为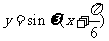 ,由图象知,
,由图象知,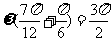 ,所以
,所以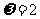 ,因此选C.
,因此选C.
点评:把按照向量平移转化为方向平移,再利用函数图象的平移规律“左加右减,上加下减”来解决问题.
例5. 已知向量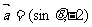 与
与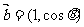 互相垂直,其中
互相垂直,其中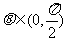 .
.
(1)求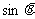 和
和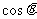 的值;
的值;
(2)若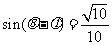 ,
,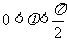 ,求
,求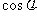 的值.
的值.
解析:(1)∵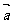 与
与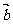 互相垂直,则
互相垂直,则 ,即
,即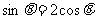 ,代入
,代入 得
得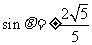 ,
,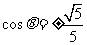 ,又
,又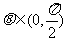 ,∴
,∴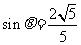 ,
,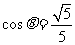 .
.
(2)∵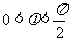 ,
,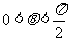 ,∴
,∴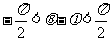 ,则
,则 ,
,
∴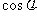

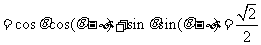 .
.
点评:该题以向量为载体考查了三角函数的基本运算性质和向量的数量积.三角函数与平面向量的综合题在近几年的高考题中经常出现,难度不大,考题灵活多变,形式新颖,较好的考查了这两部分的基本知识和基本方法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com