
1. 三角函数图象与性质的综合
正、余弦函数在[0,2π],正切函数在(-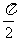 ,
,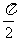 )的图象及性质,如单调性、最大值与最小值、有界性、对称性、周期性、图象与x轴的交点、函数图象平移的规律等一直是高考的重要内容.考查的形式通常是综合考查,以选择题、解答题为主,难度以容易题、中档题为主.
)的图象及性质,如单调性、最大值与最小值、有界性、对称性、周期性、图象与x轴的交点、函数图象平移的规律等一直是高考的重要内容.考查的形式通常是综合考查,以选择题、解答题为主,难度以容易题、中档题为主.
例1.将函数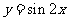 的图象向左平移
的图象向左平移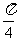 个单位, 再向上平移1个单位,所得图象的函数解析式是( )
个单位, 再向上平移1个单位,所得图象的函数解析式是( )
A.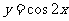 B.
B.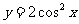 C.
C.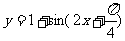 D.
D.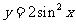
答案:B
解析:将函数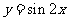 的图象向左平移
的图象向左平移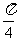 个单位,得到函数
个单位,得到函数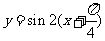 即
即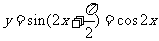 的图象,再向上平移1个单位,所得图象的函数解析式为
的图象,再向上平移1个单位,所得图象的函数解析式为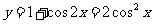 ,故选B.
,故选B.
点评:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的基本知识和基本技能,其中公式的变形在解决本题中起着很重要的作用.
例2.如果函数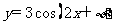 的图象关于点
的图象关于点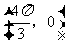 中心对称,那么
中心对称,那么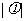 的最小值为( )
的最小值为( )
(A)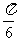 (B)
(B)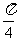 (C)
(C)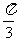 (D)
(D) 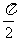
答案:C
解析:  函数
函数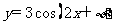 的图象关于点
的图象关于点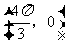 中心对称,
中心对称,
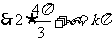
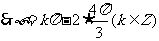 .由此易得
.由此易得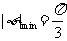 .故选C.
.故选C.
点评:该题考查了三角函数的图象和性质,对于三角函数图象的对称问题,要注意五点作图法中的五个基本点的坐标和整体思想的运用.
例3.已知函数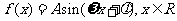 (其中
(其中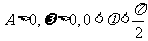 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为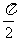 ,且图象上一个最低点为
,且图象上一个最低点为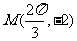 .
.
(Ⅰ)求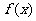 的解析式;
的解析式;
(Ⅱ)当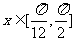 ,求
,求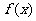 的值域.
的值域.
解析:(1)由最低点为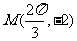 得A=2.
得A=2.
由x轴上相邻的两个交点之间的距离为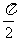 得
得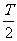 =
=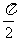 ,即
,即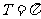 ,
,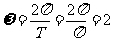 .
.
由点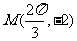 在图象上的
在图象上的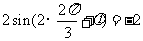 ,即
,即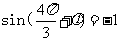 .
.
故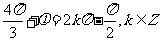
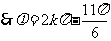 .
.
又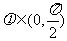 ,
,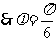 ,故
,故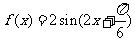 .
.
(2)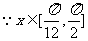 ,
,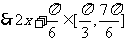
当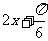 =
=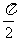 ,即
,即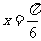 时,
时,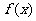 取得最大值2;
取得最大值2;
当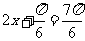 ,即
,即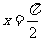 时,
时,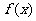 取得最小值-1,
取得最小值-1,
故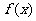 的值域为[-1,2].
的值域为[-1,2].
点评:该题综合考查了三角函数的图象和性质,对于三角函数图象的准确把握和对其性质的准确理解是解决该题必不可少的条件,求函数的值域时,一定要注意自变量的取值范围.
2.对该部分内容一般以选择、解答题的形式进行考查,且难度不大,主要考查以下四类问题:(1)与三角函数单调性有关的问题;(2)与三角函数图象有关的问题;(3)应用同角三角函数的基本关系和诱导公式求三角函数值及化简和等式证明的问题;(4)与周期有关的问题.
[知识交汇]
1.高考对该部分的考查主要是三角函数的图象与性质,对三角恒等变换的考查难度有所降低,解三角形是一个知识交汇点,将三角、向量、平面几何等知识综合起来考查.要求能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的问题.
3. 讨论关于x的方程lg(x-1)+lg(3-x)=lg(a-x)的实根个数.
2.已知函数f(x)=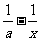 (a>0,x>0).
(a>0,x>0).
(1)求证:f(x)在(0,+∞)上是增函数;
(2)若f(x)≤2x在(0,+∞)上恒成立,求a的取值范围;
(3)若f(x)在[m,n]上的值域是[m,n](m≠n),求a的取值范围.
1.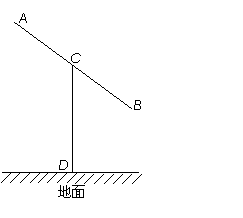 某建筑的金属支架如图所示,根据要求
某建筑的金属支架如图所示,根据要求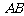 至少长2.8m,
至少长2.8m,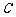 为
为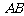 的中点,
的中点,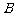 到
到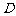 的距离比
的距离比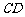 的长小0.5m,
的长小0.5m,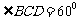 ,已知建筑支架的材料每米的价格一定,问怎样设计
,已知建筑支架的材料每米的价格一定,问怎样设计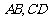 的长,可使建造这个支架的成本最低?
的长,可使建造这个支架的成本最低?
3.(1) 函数和方程是密切相关的,对于函数y=f(x),当y=0时,就转化为方程f(x)=0,也可以把函数式y=f(x)看做二元方程y-f(x)=0。函数问题(例如求函数的值域等)可以转化为方程问题来求解,方程问题也可以转化为函数问题来求解,如解方程f(x)=0,就是求函数y=f(x)的零点。
(2) 函数与不等式也可以相互转化,对于函数y=f(x),当y>0时,就转化为不等式f(x)>0,借助于函数图像与性质解决有关问题,而研究函数的性质,也离不开解不等式。
(3) 数列的通项或前n项和是自变量为正整数的函数,用函数的观点处理数列问题十分重要。
(4) 解析几何中的许多问题,例如直线和二次曲线的位置关系问题,需要通过解二元方程组才能解决,涉及到二次方程与二次函数的有关理论。
(5) 立体几何中有关线段、角、面积、体积的计算,经常需要运用布列方程或建立函数表达式的方法加以解决。
[思想方法]
[例1](2009年高考山东卷理科第20题)
等比数列{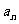 }的前n项和为
}的前n项和为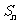 ,已知对任意的
,已知对任意的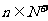 ,点
,点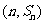 ,均在函数
,均在函数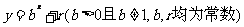 的图像上.
的图像上.
(Ⅰ)求r的值;
(Ⅱ)当b=2时,记 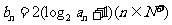
证明:对任意的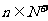 ,不等式
,不等式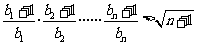 成立
成立
[解析](Ⅰ) 由题意知: 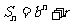 ,
,
当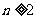 时,
时,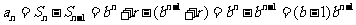 ,
,
由于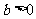 且
且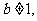 所以当
所以当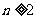 时, {
时, {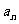 }是以
}是以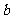 为公比的等比数列,
为公比的等比数列,
又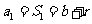 ,
,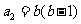 ,
,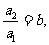 即
即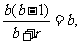 解得
解得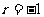 .
.
(Ⅱ)∵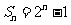 ,∴当
,∴当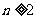 时,
时,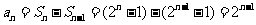 ,
,
又当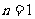 时,
时, 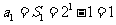 ,适合上式,∴
,适合上式,∴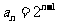 ,
,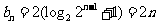 ,
,
∴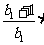
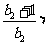
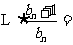
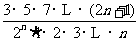 ,
,
下面用数学归纳法来证明不等式: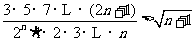
证明:(1)当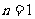 时,左边=
时,左边=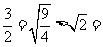 右边,不等式成立.
右边,不等式成立.
(2)假设当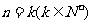 时,不等式成立,即
时,不等式成立,即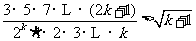 ,
,
则当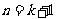 时,
时,
不等式左边=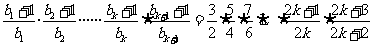

所以当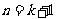 时,不等式也成立,
时,不等式也成立,
综上(1)(2)可知:当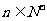 时,不等式
时,不等式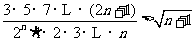 恒成立,
恒成立,
所以对任意的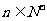 ,不等式
,不等式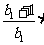
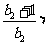
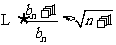 成立.
成立.
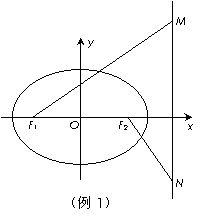 [例2]如图,椭圆
[例2]如图,椭圆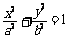 (a>b>0)的左、右焦点分别为F1、F2,M、N是椭圆右准线上的两个动点,且
(a>b>0)的左、右焦点分别为F1、F2,M、N是椭圆右准线上的两个动点,且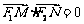 .
.
(1)设C是以MN为直径的圆,试判断原点O与圆C的位置关系;
(2)设椭圆的离心率为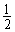 ,MN的最小值为
,MN的最小值为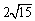 ,求椭圆方程.
,求椭圆方程.
[解](1)设椭圆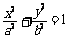 的焦距为2c(c>0),
的焦距为2c(c>0),
则其右准线方程为x=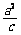 ,且F1(-c, 0), F2(c, 0). 、
,且F1(-c, 0), F2(c, 0). 、
设M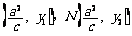 ,
,
则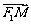 =
=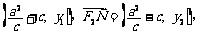
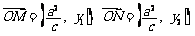 .
.
因为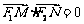 ,所以
,所以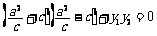 ,即
,即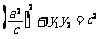 .
.
于是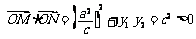 ,故∠MON为锐角.
,故∠MON为锐角.
所以原点O在圆C外.
(2)因为椭圆的离心率为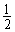 ,所以a=2c,
,所以a=2c,
于是M 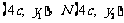 ,且
,且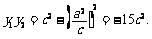
MN2=(y1-y2)2=y12+y22-2y1y2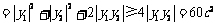 .
.
当且仅当
y1=-y2=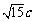 或y2=-y1=
或y2=-y1=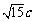 时取“=”号,
时取“=”号,
所以(MN)min= 2c=2,于是c=1, 从而a=2,b=,
故所求的椭圆方程是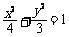 .
.
[例3]已知函数f(x)=x2–(m+1)x+m(m∈R)
(1)若tanA,tanB是方程f(x)+4=0的两个实根,A、B是锐角三角形ABC的两个内角.求证:m≥5;
(2)对任意实数α,恒有f(2+cosα)≤0,证明m≥3;
(3)在(2)的条件下,若函数f(sinα)的最大值是8,求m.
解析:(1)证明:f(x)+4=0即x2–(m+1)x+m+4=0.依题意:
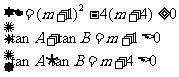 又A、B锐角为三角形内两内角
又A、B锐角为三角形内两内角
∴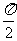 <A+B<π
<A+B<π
∴tan(A+B)<0,即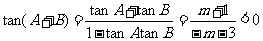
∴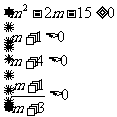 ∴m≥5
∴m≥5
(2)证明:∵f(x)=(x–1)(x–m)
又–1≤cosα≤1,∴1≤2+cosα≤3,恒有f(2+cosα)≤0
即1≤x≤3时,恒有f(x)≤0即(x–1)(x–m)≤0
∴m≥x但xmax=3,∴m≥xmax=3
(3)解:∵f(sinα)=sin2α–(m+1)sinα+m=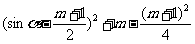
且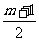 ≥2,∴当sinα=–1时,f(sinα)有最大值8.
≥2,∴当sinα=–1时,f(sinα)有最大值8.
即1+(m+1)+m=8,∴m=3
[例4]某厂家拟在2009年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)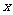 万件与年促销费用
万件与年促销费用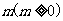 万元满足
万元满足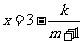 (
(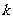 为常数),如果不搞促销活动,则该产品的年销售量是1万件. 已知2009年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
为常数),如果不搞促销活动,则该产品的年销售量是1万件. 已知2009年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
(1)将2009年该产品的利润y万元表示为年促销费用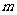 万元的函数;
万元的函数;
(2)该厂家2009年的促销费用投入多少万元时,厂家的利润最大?
解:(1)由题意可知,当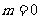 时,
时,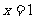 ,∴
,∴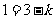 即
即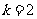 ,
,
∴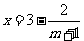 ,每件产品的销售价格为
,每件产品的销售价格为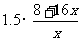 元.
元.
∴2009年的利润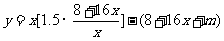
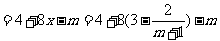
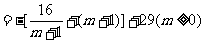
(2)∵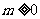 时,
时,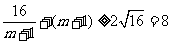 .
.
∴ ,当且仅当
,当且仅当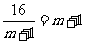 ,即
,即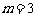 时,
时,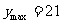 .
.
答:该厂家2009年的促销费用投入3万元时,厂家的利润最大,最大为21万元.
[专题演练]
2.方程的思想,就是分析数学问题中变量间的等量关系,建立方程或方程组,或者构造方程,通过解方程或方程组,或者运用方程的性质去分析、转化问题,使问题获得解决。方程的数学是对方程概念的本质认识,用于指导解题就是善于利用方程或方程组的观点观察处理问题。方程思想是动中求静,研究运动中的等量关系.
1.函数的思想,是用运动和变化的观点,分析和研究数学中的数量关系,建立函数关系或构造函数,运用函数的图像和性质去分析问题、转化问题,从而使问题获得解决。函数思想是对函数概念的本质认识,用于指导解题就是善于利用函数知识或函数观点观察、分析和解决问题。
7.已知函数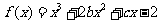 的图象在与
的图象在与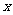 轴交点处的切线方程是
轴交点处的切线方程是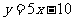 .
.
(I)求函数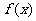 的解析式;
的解析式;
(II)设函数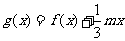 ,若
,若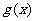 的极值存在,求实数
的极值存在,求实数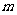 的取值范围以及函数
的取值范围以及函数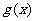 取得极值时对应的自变量
取得极值时对应的自变量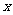 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com