
21. (本小题满分12分)
已知中心在坐标原点的双曲线的一条准线方程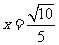 ,且它的渐近线与圆
,且它的渐近线与圆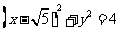 相切。
相切。
(I)求双曲线的方程;
(II)若过点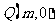 (为非零常数)的直线
(为非零常数)的直线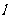 与双曲线相交于不同于双曲线顶点的两点
与双曲线相交于不同于双曲线顶点的两点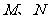 ,且
,且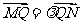 ,问在轴上是否存在定点
,问在轴上是否存在定点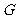 ,使
,使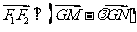 ?若存在,求出定点
?若存在,求出定点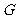 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
20. (本小题满分12分)
已知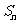 是正整数列
是正整数列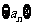 的前项和,
的前项和,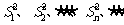 是以3为首项,以1为公差的等差数列,数列
是以3为首项,以1为公差的等差数列,数列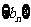 为无穷等比数列,其前四项之和为120,第二项与第四项之和为90.
为无穷等比数列,其前四项之和为120,第二项与第四项之和为90.
(I)求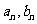 ;
;
(II)试从数列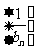 中挑出一些项构成一个无穷等比数列,使它的各项和等于
中挑出一些项构成一个无穷等比数列,使它的各项和等于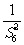 ,并指出所挑出数列的首项和公比。
,并指出所挑出数列的首项和公比。
19. (本小题满分12分)
如图,四棱锥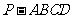 的底面是正方形,
的底面是正方形,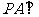 底面
底面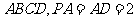 ,点
,点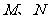 分别在棱
分别在棱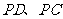 上,且
上,且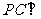 面
面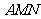 。
。
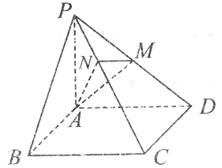 (I)求二面角
(I)求二面角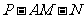 的大小;
的大小;
(II)求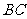 与面
与面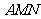 所成角。
所成角。
18. (本小题满分12分)
在某次知识抢答赛的预赛中,甲乙两位同学分在同一组(每组两人),主持人给每个组出三个必答题,每次只可由一位选手作答,每个组只有答对不少于两道题才有资格进入决赛,已知对每道题,甲回答正确的概率为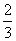 ,乙回答正确的概率为
,乙回答正确的概率为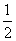 ,比赛规则规定可任选一位同学答第一题,如果某个同学回答正确,则仍由他继续回答下一道题,如果该同学答错了,则下一题就由另一位同学来回答,且每个同学答题的行为是相互独立的。甲乙两人决定先由甲来回答第一题。
,比赛规则规定可任选一位同学答第一题,如果某个同学回答正确,则仍由他继续回答下一道题,如果该同学答错了,则下一题就由另一位同学来回答,且每个同学答题的行为是相互独立的。甲乙两人决定先由甲来回答第一题。
(I)求甲乙两同学所在组晋级决赛的概率;
(II)以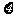 表示甲乙两同学所在组答对题目的个数,求
表示甲乙两同学所在组答对题目的个数,求 .
.
17. 在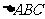 中,
中,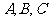 分别是
分别是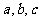 的对边长,已知
的对边长,已知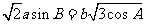 。
。
(I)求角的值;
(II)若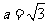 ,求
,求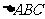 面积的最大值。
面积的最大值。
16. 设函数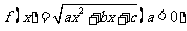 的定义域,若所有点
的定义域,若所有点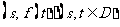 构成一个正方形区域,则
构成一个正方形区域,则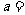 。
。
15. 若函数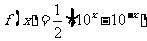 的反函数
的反函数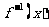 ,则
,则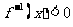 的解为
。
的解为
。
14. 过抛物线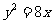 的焦点的弦
的焦点的弦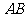 以
以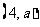 为中点,则
为中点,则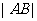 =
。
=
。
13.将函数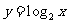 的图象按向量
的图象按向量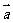 平移后,得到函数
平移后,得到函数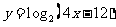 的图象,则
的图象,则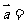
。
12. 有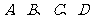 四人依次站在正方形的四个顶点上传球,从开始,每次可随意传给相邻的两人之一,则传完8次时,球又被传回的概率为
四人依次站在正方形的四个顶点上传球,从开始,每次可随意传给相邻的两人之一,则传完8次时,球又被传回的概率为
A、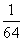 B、
B、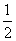 C、
C、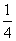 D、
D、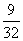
第II卷(非选择题,共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com