
22.(本题12分)已知函数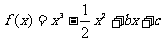 ,且
,且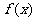 在
在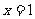 处取得极值.
处取得极值.
(1)求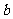 的值;
的值;
(2)若当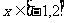 时,
时,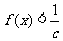 恒成立,求
恒成立,求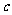 的取值范围;
的取值范围;
(3)若集合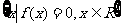 有且只有一个元素,求
有且只有一个元素,求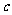 的取值范围.
的取值范围.
昆明第一中学2009-2010 学年度下学期期末考试
21.(本题12分)2010年全国普通高等学校招生中,某校有5名体育考生到某高校考点参加体育专业达标测试,并指派1名指导教师带队.
(1)若他们乘公共汽车前往,汽车内恰好有前后两排各3个空座位,求指导教师不坐在后排的概率;
(2)若每名考生测试达标的概率都是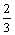 (相互独立),测试后有r人达标,经计算5人中恰有r人同时达标的概率是
(相互独立),测试后有r人达标,经计算5人中恰有r人同时达标的概率是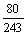 ,求r值.
,求r值.
20.(本题12分)口袋中有质地、大小完全相同的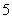 个球,编号分别为
个球,编号分别为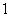 、
、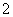 、
、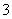 、
、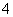 、
、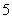 ,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢。
,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢。
(1)求两个编号的和为6的概率;
(2)求甲赢的事件发生的概率。
19.(本题12分)甲、乙两个车间分别制作一种零件,在自动包装传送带上每隔10分钟抽取一件产品,测其质量,分别记录抽查的数据如下:甲:102, 101, 99, 98, 103, 98, 99;乙:105, 102, 97, 92, 96, 101, 107;(1)这种抽样方法是什么抽样?(2)估计甲、乙两个车间产品质量的平均值与方差,并分析哪个车间的产品较稳定;(3)如果产品质量在区间(95,105)内为合格,那么这个工厂生产的产品合格率是多少?
18.(本题12分)已知函数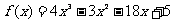 .
.
(1)求函数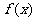 的图象在
的图象在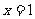 处的切线方程;
处的切线方程;
(2)求函数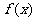 在
在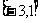 上的最值.
上的最值.
17.(本题10分)已知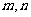 是正整数,在
是正整数,在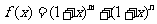 中的
中的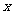 系数为
系数为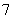 .
.
(1)求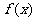 的展开式中
的展开式中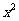 的系数的最小值
的系数的最小值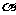 ;
;
(2)当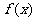 的展开式中的
的展开式中的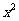 系数为
系数为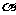 时,求
时,求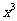 的系数
的系数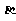 .
.
16.已知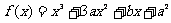 在时有极值
在时有极值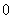 ,
,
则 .
.
15.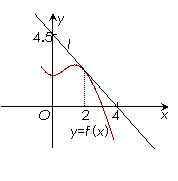 如图,函数
如图,函数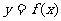 的图象在点P处的切线是
的图象在点P处的切线是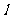 ,
,
则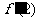 = .
= .
14.先后抛掷两枚均匀的正方体骰子,骰子朝上的面的点数为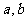 ,则
,则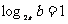 的概率为
.
的概率为
.
13.已知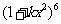 (
(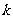 是正整数)的展开式中,
是正整数)的展开式中,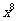 的系数小于120,则
的系数小于120,则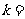 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com