36．(30分)青藏高原(北纬25°-40°,东经74°-104°)是世界上最高的高原,平均海拔高度在4000米以上,有"世界屋脊"和"世界第三极"之称．回答下列问题．

　 (1)青藏高原是这样形成的？(4分)

　 (2)简述太阳能的特点;简析青藏地区太阳能丰富的原因。(10分)

　 (3)青藏高原为什么被称为"亚洲水塔"？(4分)

　 (4)简要说明青藏地区的河谷农业主要分布地区、主要农作物及分布原因。(12分)

21．(本小题满分14分)

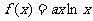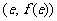　　　　 已知函数图像上点处的切线方程为与直线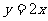平行(其中)，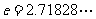

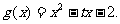
　 (I)求函数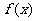的解析式；

　 (II)求函数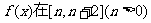上的最小值；

　 (III)对一切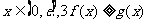恒成立，求实数t的取值范围.

20．(本小题满分13分)

　　　　 已知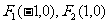是椭圆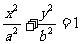的两个焦点，点G与F₂关于直线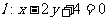对称，且GF₁与l的交点P在椭圆上.

　 (I)求椭圆方程；

　 (II)若P、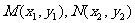的椭圆上的不同三点，直线PM、PN的倾斜角互补，问直线MN的斜率是否是定值？如果是，求出该定值，如果不是，说明理由.

19．(本小题满分12分)

　　　　 已知数列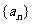的首项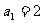，其前n项和为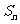，当时，满足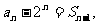

　　 又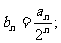

　 (I)证明：数列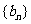是等差数列；

　 (II)求数列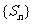的前n项和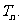

18．(本小题满分12分)

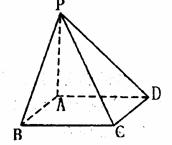
　　 已知四棱锥P-ABCD的侧棱PA⊥平面ABCD，底面ABCD为正方形，且AB=AP=a.

　 (I)若E、F分别是PA、BC的中点，证明EF//平面PCD；

　 (II)若G为AB中点，求证：二面角G-PC-D的大小为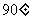

17．(本小题满分12分)

　　　　 某校选派4人参加上级组织的数学竞赛，现从甲、乙两个竞赛班各选派2人.设甲、乙两班选派的人员获奖概率分别为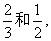且4位选手是否获奖互不影响.

　 (I)求甲、乙两班各有1人获奖的概率；

　 (II)求该校获奖人数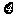的分布列与期望.

16．(本小题满分12分)

　　　　 在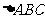中，角A、B、C的对边分别为a、b、c，且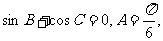BC边上的中线AM的长为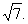

　 (I)求角B的大小；

　 (II)求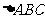的面积.

15．选做题(考生只能从A、B、C题中选作一题)

　　 A、已知直线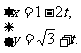(t为参数)与圆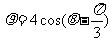相交于A、B两点，则|AB|=

　　　　 　　　　　　　　　　.

　　 B、若关于x的方程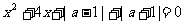有实根，

则实数a的取值范围为　　 .　　

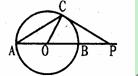
C、如图，⊙O的直径AB=6cm，P是延长线上的一点，过

点P作⊙O的切线，切点为C，连结AC，若，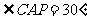

则PC=　　　　 .

14．在区间[0，2]上随机取一个数x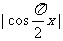，的值介于0到0.5之间的概率为　　　　　　 .

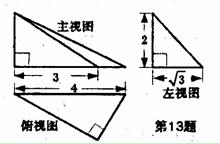
13．一个棱锥的三视图如图，则该棱锥的全面积(单位：cm²)为　　　　 .