
6.从集合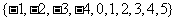 中选出5个数组成子集,使得这5个数中的任意两数之k*s#5^u和不等于1,则取出这样的子集的概率为( )
中选出5个数组成子集,使得这5个数中的任意两数之k*s#5^u和不等于1,则取出这样的子集的概率为( )
A.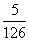 B.
B.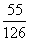
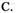
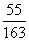 D.
D.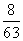
5. 条件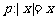 ,条件
,条件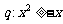 ,则p是q的( )
,则p是q的( )
A.充分不必要条件 B.必要不充分条件
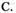 充要条件 D.既不充分又不必要条件
充要条件 D.既不充分又不必要条件
4.已知点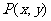 是
是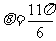 角的终边上的任意一点,则
角的终边上的任意一点,则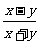 的值等于( )
的值等于( )
A.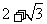 B.
B.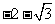
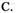
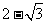 D.
D.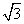
3. 若直线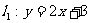 ,直线
,直线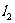 与
与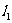 关于直线
关于直线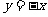 对称,则直线
对称,则直线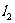 的斜率为 ( )
的斜率为 ( )
A.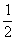 B.
B.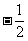
 D.
D.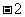
2.函数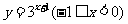 的反函数是(
)
的反函数是(
)
A.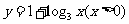 B.
B.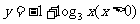
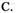
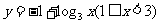 D.
D.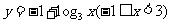
1.不等式 的解集是( )
的解集是( )
A.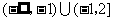 B.
B.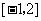
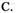
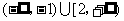 D.
D.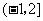
21.(本小题满分13分)
已知函数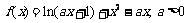 ,
,
(Ⅰ)若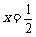 是函数
是函数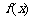 的一个极值点,求
的一个极值点,求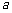 ;
;
(Ⅱ)讨论函数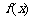 的单调区间;
的单调区间;
(Ⅲ)若对于任意的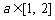 ,不等式
,不等式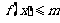 在
在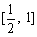 上恒成立,求
上恒成立,求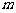 的取值范围.
的取值范围.
解:(Ⅰ)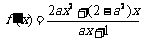 ……………………………………………1分
……………………………………………1分
因为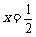 是函数
是函数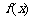 的一个极值点,所以
的一个极值点,所以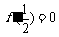 ,得
,得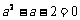 .
.
因为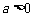 ,所以
,所以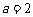 . ……………………………………………………3分
. ……………………………………………………3分
(Ⅱ)因为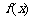 的定义域是
的定义域是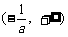 ,
,
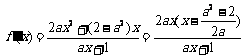 .
.
(1) 当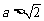 时,列表
时,列表
 |
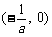 |
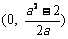 |
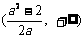 |
 |
+ |
- |
+ |
 |
增 |
减 |
增 |
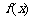 在
在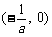 ,
,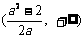 是增函数;
是增函数;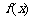 在
在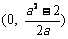 是减函数.
是减函数.
(2)
当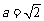 时,
时,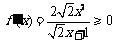 ,
,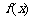 在
在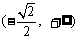 是增函数.
是增函数.
(3) 当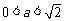 时,列表
时,列表
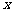 |
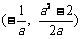 |
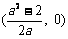 |
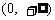 |
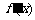 |
+ |
- |
+ |
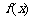 |
增 |
减 |
增 |
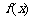 在
在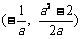 ,
,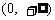 是增函数;
是增函数;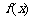 在
在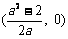 是减函数. ……7分
是减函数. ……7分
(Ⅲ)当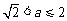 时,
时,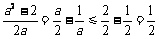 ,
,
由(Ⅱ)可知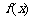 在
在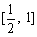 上是增函数.
上是增函数.
当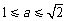 时,也有
时,也有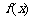 在
在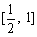 上是增函数,
上是增函数,
所以对于任意的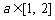 ,
,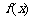 的最大值为
的最大值为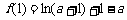 ,
,
要使不等式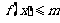 在
在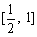 上恒成立,
上恒成立,
须 ,
,
记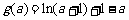 ,因为
,因为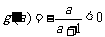 ,
,
所以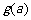 在
在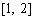 上递减,
上递减,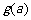 的最大值为
的最大值为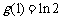 ,所以
,所以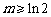 .
.
故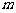 的取值范围为
的取值范围为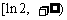 .
…………………………………………10
.
…………………………………………10
20.(本小题满分13分)
已知过点A(0,1),且方向向量为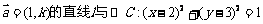 ,相交于M、N两点.
,相交于M、N两点.
(1)求实数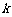 的取值范围;
的取值范围;
(2)求证: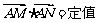 ;
;
(3)若O为坐标原点,且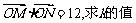 .
.
解:(1)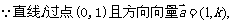
 ……………………2分
……………………2分
由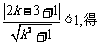
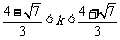 ……………………4分
……………………4分
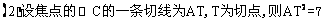
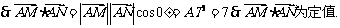 ……………………8分
……………………8分
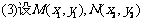
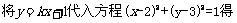
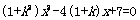 ……………………10分
……………………10分
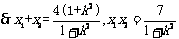 ……………………
……………………
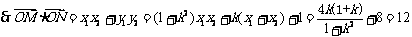
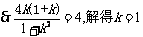
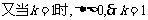 ……………………13分
……………………13分
19.(本小题满分13分)
已知数列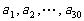 ,其中
,其中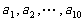 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;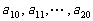 是公差为
是公差为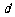 的等差数列;
的等差数列;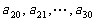 是公差为
是公差为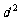 的等差数列(
的等差数列(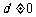 ).
).
(1)若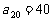 ,求
,求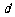 ;
;
(2)试写出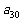 关于
关于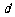 的关系式,并求
的关系式,并求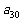 的取值范围;
的取值范围;
(3)续写已知数列,使得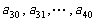 是公差为
是公差为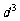 的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
[解](1)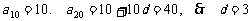 .
…… 2分
.
…… 2分
(2)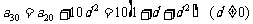 ,
…… 分
,
…… 分
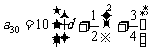 ,
,
当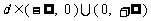 时,
时,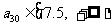 .
…… 5分
.
…… 5分
(3)所给数列可推广为无穷数列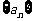 ,其中
,其中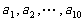 是首项为1,公差为1的等差数列,当
是首项为1,公差为1的等差数列,当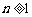 时,数列
时,数列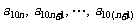 是公差为
是公差为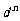 的等差数列. …… 7分
的等差数列. …… 7分
研究的问题可以是:试写出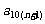 关于
关于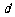 的关系式,并求
的关系式,并求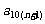 的取值范围.……8 分
的取值范围.……8 分
研究的结论可以是:由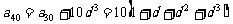 ,
,
依次类推可得 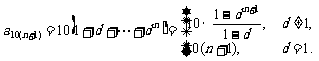
当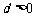 时,
时,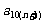 的取值范围为
的取值范围为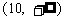 等.
…… 10分
等.
…… 10分
18.(本小题满分12分)
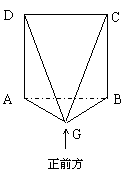 如图,四棱锥G—ABCD中,ABCD是正方形,且边长为2a,面ABCD⊥面ABG,AG=BG。
如图,四棱锥G—ABCD中,ABCD是正方形,且边长为2a,面ABCD⊥面ABG,AG=BG。
(1)画出四棱锥G—ABCD的三视图;
(2)在四棱锥G—ABCD中,过点B作平面
AGC的垂线,若垂足H在CG上,
求证:面AGD⊥面BGC
(3)在(2)的条件下,求三棱锥D—ACG的体积
及其外接球的表面积。
解:(1)三视图(见右图)………………3分
(2)ABCD是正方形 ∴ BC⊥AB
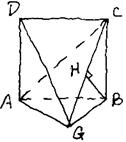 ∵面ABCD⊥面ABG ∴ BC⊥面ABG
∵面ABCD⊥面ABG ∴ BC⊥面ABG
∵AG 面ABG ∴
BC⊥AG
面ABG ∴
BC⊥AG
又 BH⊥面AGC ∴ BH⊥AG
∵ BC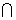 BH=B ∴
AG⊥面AGD
BH=B ∴
AG⊥面AGD
∴面AGD⊥面BGC …………………………7分
(3)由(2)知 AG⊥面BGC ∴AG⊥BG 又AG=BG
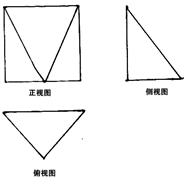 ∴ △ABG是等腰Rt△,取AB中点E,
∴ △ABG是等腰Rt△,取AB中点E,
连结GE,则GE⊥AB
∴ GE⊥面ABCD
∴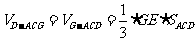
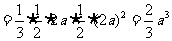 ………………9分
………………9分
又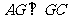 ∴ 取AC中点M,则
∴ 取AC中点M,则 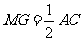 因此:
因此:
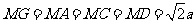 即点M是三棱锥D—ACG的外接球的球心,
即点M是三棱锥D—ACG的外接球的球心,
半径为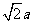 ∴
∴ 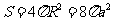 ……………………14分
……………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com