
22. (本小题满分14分)
已知定义在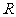 上的单调函数
上的单调函数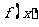 ,存在实数
,存在实数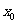 使得对任意实数
使得对任意实数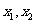 ,总有
,总有
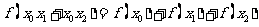 恒成立。
恒成立。
①求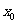 的值;
的值;
②若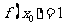 ,且对任意的正整数
,且对任意的正整数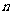 。有
。有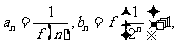
记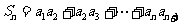 ,
,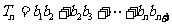 ,比较
,比较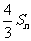 与
与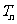 的大小关系,并给出证明。
的大小关系,并给出证明。
2010年临川二中、新余四中高三联考
21.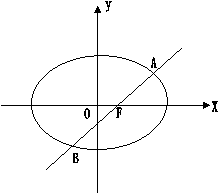 (小题满分12分)已知椭圆
(小题满分12分)已知椭圆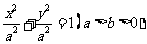 的离心率为
的离心率为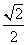 ,右焦点为
,右焦点为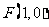 ,直线
,直线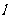 经过点
经过点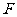 且与椭圆交于
且与椭圆交于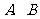 两点,
两点,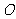 为坐标原点。
为坐标原点。
①求椭圆的方程;
②若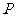 是椭圆上的一个动点,求
是椭圆上的一个动点,求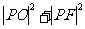 的最大值和最小值;
的最大值和最小值;
③当直线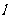 绕点
绕点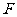 转动时,试问:在
转动时,试问:在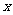 轴上是否存在定点
轴上是否存在定点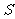 ,使
,使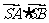 为常数,若存在,求出定点
为常数,若存在,求出定点 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
20. (本小题满分12分)已知函数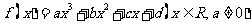 ,-2是
,-2是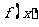 的一个零点,又
的一个零点,又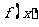 在
在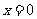 处有极值,在区间
处有极值,在区间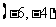 和
和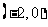 上是单调的,且在这两个区间上的单调性相反。
上是单调的,且在这两个区间上的单调性相反。
①求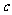 的值;
的值;
②求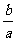 的取值范围;
的取值范围;
③当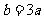 时,求使
时,求使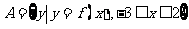 ,
,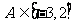 成立的实数
成立的实数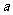 的取值范围。
的取值范围。
19.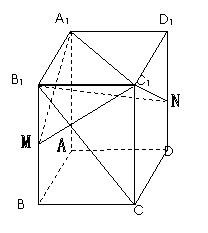 (本小题满分12分)(如图)在正四棱柱
(本小题满分12分)(如图)在正四棱柱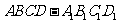 中,
中,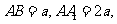
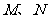 分别是棱
分别是棱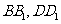 的中点。
的中点。
①求异面直线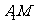 与
与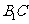 所成的角的余弦值;
所成的角的余弦值;
②若正四棱柱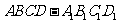 的体积为
的体积为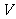 ,三棱锥
,三棱锥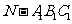 的体积为
的体积为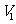 ,求
,求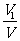 的值。
的值。
③求平面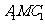 与平面
与平面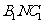 所成的二面角的大小。
所成的二面角的大小。
18. (本小题满分12分)为迎接2010年上海世界博览会的召开,上海某高校对本校报名参加志愿者服务的学生进行英语、日语口语培训,每名志愿者可以选择参加一项培训、参加两项培训或不参加培训。已知参加过英语培训的有75%,参加过日语培训的有60%,假设每名志愿者对培训项目的选择是相互独立的,且各人的选择相互之间没有影响。
⑴从该高校志愿者中任选1名,求这人参加过本次口语培训的概率;
⑵从该高校志愿者中任选3名,求至少有2人参加过本次口语培训的概率。
17.(本小题满分12分)在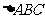 中,
中,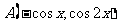 ,
,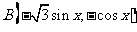 ,
,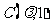 ,
,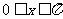 ,若
,若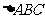 的重心在
的重心在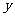 轴的负半轴上。
轴的负半轴上。
① 求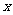 的取值范围;
的取值范围;
② 求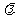 的取值范围。
的取值范围。
16.对于在区间 上有意义的两个函数
上有意义的两个函数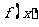 与
与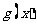 ,如果对于任意的
,如果对于任意的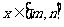 ,均有
,均有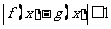 ,则称
,则称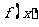 与
与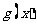 在
在 上是接近的,若函数
上是接近的,若函数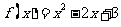 与
与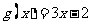 在区间
在区间 上是接近的,给出如下区间:①
上是接近的,给出如下区间:①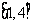 ②
②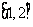
③ 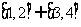 ④
④ 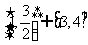 ,则区间
,则区间 可以是
(把你认为正确的序号都填上)
可以是
(把你认为正确的序号都填上)
15.在正三棱锥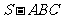 中,
中,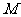 为棱
为棱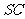 上异于端点的点,且
上异于端点的点,且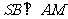 ,若侧棱SA=
,若侧棱SA=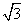 ,则正三棱锥
,则正三棱锥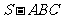 的外接球的表面积是
的外接球的表面积是
14.已知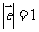 ,且满足
,且满足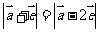 ,则向量
,则向量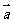 在
在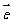 方向上的投影等于
方向上的投影等于
13.若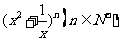 的二项展开式中第5项为常数项,则
的二项展开式中第5项为常数项,则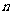 =
=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com