
16. 美国太空总署(NASA)为探测月球是否存在水分,于2009年10月9日利用一支火箭和一颗卫星连续撞击月球. 据天文学家测量,月球的半径约为l 800 km,月球表面的重力加速度约为地球表面重力加速度的1/6,月球表面在阳光照射下的温度可达127℃ ,而此时水蒸气分子的平均速率达2 km/s,下列说法正确的是
A. 卫星撞月前应先在原绕月轨道上减速
B. 卫星撞月前应先在原绕月轨道上加速
 由于月球的第一宇宙速度大于2 km/s,所以月球表面可能有水
由于月球的第一宇宙速度大于2 km/s,所以月球表面可能有水
D. 由于月球的第一宇宙速度小于2 km/s,所以月球表面在阳光照射下不可能有水
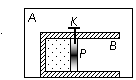
15. 如图所示,在固定的真空容器A内部固定着一个绝热气缸B,用质量为m的绝热活塞P将一部分理想气体封闭在气缸内。撤去销子K,不计摩擦阻力,活塞将向右运动。该过程
 A. 活塞做匀加速运动,缸内气体温度不变
A. 活塞做匀加速运动,缸内气体温度不变
B. 活塞做匀加速运动,缸内气体温度降低
 活塞做变加速运动,缸内气体温度降低
活塞做变加速运动,缸内气体温度降低
D. 活塞做变加速运动,缸内气体温度不变
14. 三个原子核X、Y、Z,X核放出一个正电子后变为Y核,Y核与质子发生核反应后生成Z核并放出一个氦核,则下面说法正确的是
A. X核比Z核多一个质子 B. X核比Z核少一个中子
 X核与Z核的总电荷是Y核电荷的3倍 D. X核的质量数比Z核质量数大3
X核与Z核的总电荷是Y核电荷的3倍 D. X核的质量数比Z核质量数大3
(17)(本小题满分10分)
向量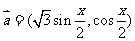 ,
,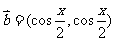 ,记
,记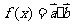 ,当
,当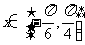 时, 试求
时, 试求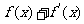 的值域.
的值域.
(18) (本小题满分12分)
已知袋中装有大小、形状完全相同的m个红球k*s#5^u和n个白球,其中m、n满足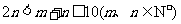 ,若从中任取2个球,取出的2个球是同色的概率等于取出的2个球是异色的概率.
,若从中任取2个球,取出的2个球是同色的概率等于取出的2个球是异色的概率.
(Ⅰ) 求m、n的值;
(Ⅱ) 当m>4时,从袋中任取3个球,设取到红球的个数为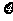 ,求
,求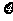 的分布列及数学期望.
的分布列及数学期望.
(19) (本小题满分12分)
|
|
|
|




 如图,侧棱垂直底面的三棱柱
如图,侧棱垂直底面的三棱柱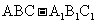 的底面ABC位于平行四边形ACDE中,AE=2,
的底面ABC位于平行四边形ACDE中,AE=2,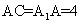 ,
,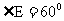 ,点B为DE中点.
B1
,点B为DE中点.
B1
|
|
|





 (Ⅰ) 求证:平面
(Ⅰ) 求证:平面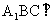 平面
平面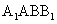 ;
;
(Ⅱ) 设二面角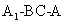 的大小为
的大小为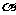 ,直线AC与平面
,直线AC与平面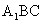 所成的角为
所成的角为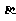 ,求
,求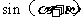 的值.
的值.
(20) (本小题满分12分)
已知数列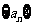 满足
满足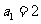 ,
,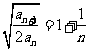 ;
;
(Ⅰ)求数列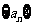 的通项公式;
的通项公式;
(Ⅱ)若数列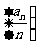 的前n项k*s#5^u和为
的前n项k*s#5^u和为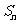 .,试比较
.,试比较 与2的大小.
与2的大小.
(21) (本小题满分12分)
已知椭圆C: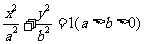 的离心率为
的离心率为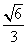 ,过右焦点F且斜率为1的直线交椭圆C于A、B两点,N为弦AB的中点.
,过右焦点F且斜率为1的直线交椭圆C于A、B两点,N为弦AB的中点.
(Ⅰ)求直线ON(O为坐标原点)的斜率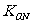 ;
;
(Ⅱ)对于椭圆C上任意一点M,试证:总存在角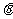
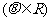 使等式:
使等式: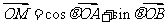 成立.
成立.
(22) (本小题满分12分)
已知函数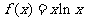 .
.
(Ⅰ)求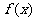 的最小值;
的最小值;
(Ⅱ)讨论关于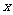 的方程
的方程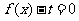 (
(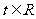 )的解的个数;
)的解的个数;
(Ⅲ)当m > o , n > o时,求证: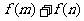 ≥
≥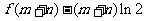 .
.
(13)已知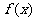 是R上的奇函数,且
是R上的奇函数,且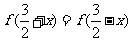 ,当
,当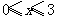 时,
时,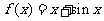 ,则
,则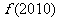 =
.
=
.
(14)已知b为二项式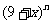 展开式中各项系数的k*s#5^u和,且
展开式中各项系数的k*s#5^u和,且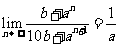 ;则实数a的取值范围是
.
;则实数a的取值范围是
.
(15)在三棱锥A-BCD中,P、Q分别是棱AC、BD上的点,连结AQ、CQ、BP、DP、PQ,若三棱锥A-BPQ、B-CPQ、C-DPQ的体积分别为6、2、8,则三棱锥A-BCD的体积为 .
(16)已知方程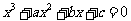 的三个实数根可分别作为一个椭圆、一双曲线、一抛物线的离心率,那么
的三个实数根可分别作为一个椭圆、一双曲线、一抛物线的离心率,那么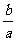 的取值范围是
.
的取值范围是
.
(1)若集合A={1,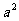 },B={2,4},则“
},B={2,4},则“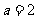 ”是“
”是“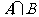 ={4}”的
={4}”的
A. 充分不必要条件 B. 必要不充分条件
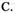 充分且必要条件
D. 既不充分也不必要条件
充分且必要条件
D. 既不充分也不必要条件
(2)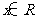 ,复数
,复数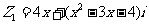 ,
,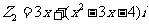 ,若
,若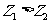 则
则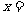
A. 0
B. 1 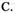 -1 D. 4
-1 D. 4
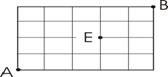 (3)如图,棋盘式街道,想从A经E到达B,若限制行进的方向只能向右或向上,则不同的走法共有
(3)如图,棋盘式街道,想从A经E到达B,若限制行进的方向只能向右或向上,则不同的走法共有
A. 126 种 B. 100种
 60 种
D. 20种
60 种
D. 20种
(4)满足条件: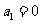 ,
,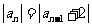 (
(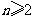 且
且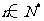 )的数列中,
)的数列中,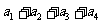 的最小值等于
的最小值等于
A. -4 B. -6 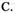 0 D. 2
0 D. 2
(5)如果直线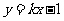 与椭圆
与椭圆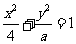 相切,那么
相切,那么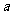 与
与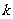 的取值范围是
的取值范围是
A. (0,1),(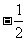 ,
,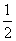 )
B.
)
B. 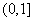 ,(
,(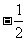 ,
,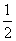 )
)
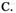 (0,1),
(0,1),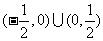 D.
D. 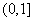 ,
,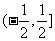
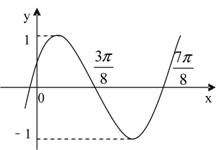 (6)已知函数
(6)已知函数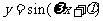 ,
,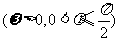 ,且此函数的图象如图所示,则点P
,且此函数的图象如图所示,则点P 的坐标为
的坐标为
(A. 2,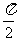 ) B. (2,
) B. (2,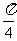 )
)
 (4,
(4,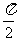 ) D. (4,
) D. (4,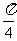 )
)
(7)异面直线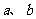 成
成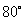 角,点
角,点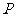 是
是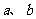 外的一定点,若过点
外的一定点,若过点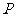 有且仅有2条直线与
有且仅有2条直线与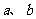 所成的角相等且等于
所成的角相等且等于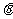 ,则
,则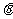 属于集合
属于集合
A. 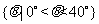 B.
B.
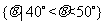
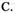
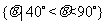 D.
D. 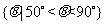
(8)已知曲线C: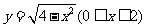 与函数
与函数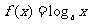 及函数
及函数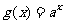 ,(其中
,(其中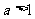 )的图像分别交于
)的图像分别交于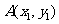 、
、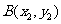 ,则
,则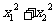 的值为
的值为
A. 16 B. 8 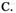 4 D. 2
4 D. 2
(9)设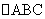 的三个内角A、B、C所对的三边分别为
的三个内角A、B、C所对的三边分别为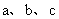 ,若
,若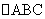 的面积
的面积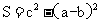 ,则
,则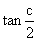 =
=
A. 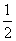 B.
B. 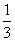
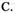
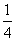 D.
D.
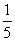
(10)对任意的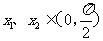 ,
,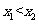 ,
,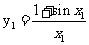 ,
,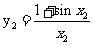 ;则
;则
A. 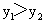 B.
B.
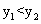
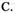
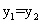 D.
无法确定
D.
无法确定
(11)已知点O是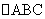 内一点,且满足
内一点,且满足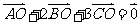 ,设Q是CO的延长线与AB的交点,记
,设Q是CO的延长线与AB的交点,记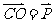 ,则
,则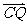 =
=
A. 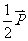 B.
B.
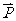
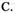
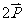 D.
D.
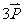
(12)抛物线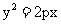
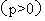 的焦点为F,点A、B在抛物线上,且
的焦点为F,点A、B在抛物线上,且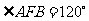 ,弦AB中点M在准线l上的射影为
,弦AB中点M在准线l上的射影为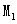 ,则
,则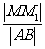 的最大值为
的最大值为
A. 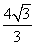 B.
B. 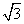
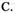
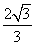 D.
D. 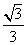
第II卷(非选择题 共90分)
21、(本小题满分14分)
解:(Ⅰ)解法一:椭圆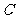 的离心率
的离心率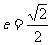 ,得
,得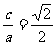 ,其中
,其中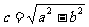 ………………1分
………………1分
椭圆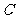 的左、右焦点分别为
的左、右焦点分别为 、
、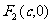 ,
………………2分又点
,
………………2分又点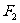 在线段
在线段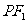 的中垂线上,
的中垂线上,
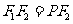 ,
………………3分
,
………………3分
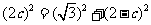 ………………4分
………………4分
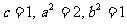 ………………5分
………………5分
椭圆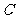 的方程为
的方程为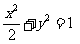 .
………………6分
.
………………6分
解法二:
椭圆 的离心率
的离心率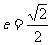 ,得
,得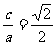 ,其中
,其中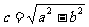 ………………1分
………………1分
椭圆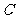 的左、右焦点分别为
的左、右焦点分别为
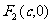 ,
………………2分
,
………………2分
设线段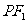 的中点为
的中点为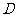 ,
,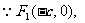
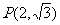 ,
,
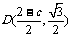 ,
………………3分
,
………………3分
又线段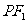 的中垂线过点
的中垂线过点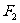 ,
,
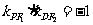 ,
………………4分
,
………………4分
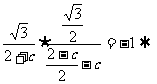
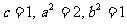 , ………………5分
, ………………5分
椭圆方程为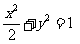 ………………6分(Ⅱ)由题意,直线
………………6分(Ⅱ)由题意,直线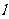 的方程为
的方程为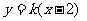 ,且
,且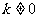 ,
………………7分
,
………………7分
联立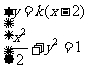 ,得
,得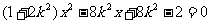 ,由
,由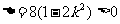 ,得
,得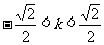 ,且
,且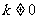 ………………8分
………………8分
设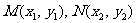 ,则有
,则有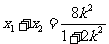 ,
,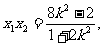 (
( ) ………………9分
) ………………9分
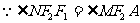 ,且由题意
,且由题意  ,
,
∴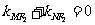 , ………………10分
, ………………10分
又∵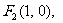
∴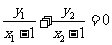 ,即
,即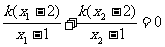 , ………………11分
, ………………11分
∴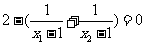 ,整理得
,整理得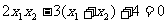 , ………………12分
, ………………12分
将( )代入得,
)代入得,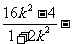
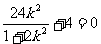 , ………………13分
, ………………13分
知上式恒成立,故直线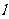 的斜率
的斜率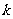 的取值范围是
的取值范围是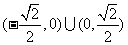 . ………………14分
. ………………14分
20、(本题满分14分)
解:(Ⅰ)设数列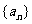 的前n项和为
的前n项和为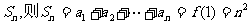 ………………1分
………………1分
当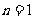 时,
时,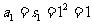 ,
………………2分
,
………………2分
当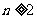 时,
时,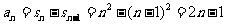 ………………3分
………………3分
∵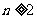 时,
时,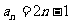 对于
对于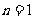 也同样适用,
也同样适用,
∴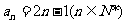 ………………4分
………………4分
(Ⅱ)n为偶数时,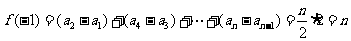 ………5分
………5分
n为奇数时,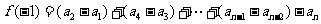
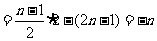 ……………… 6分
……………… 6分
∴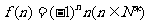 ……………… 7(Ⅲ)∵
……………… 7(Ⅲ)∵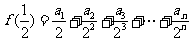
∴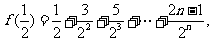 ……………… 8分 当
……………… 8分 当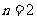 时,
时,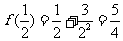 ,
……………… 9分当
,
……………… 9分当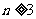 时,
时, ……………… 10分
……………… 10分
∵ …………①
…………①
∴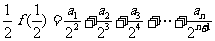 …………②
……………… 11分由①-②得
…………②
……………… 11分由①-②得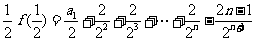
即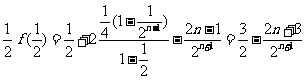
∴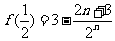 ………………
12分
………………
12分
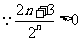
∴ 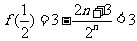 ……………… 13分
……………… 13分
所以若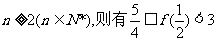 ……………… 14分
……………… 14分
19、(本小题满分14分)
解:(Ⅰ)
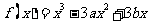
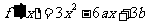 ………………2分
………………2分
由于函数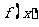 的图象与直线
的图象与直线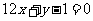 相切于点
相切于点 ,
,
所以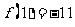 ,
,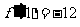 即 ………………3分
即 ………………3分
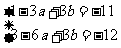 ,
………………5分
,
………………5分
解得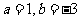 。
………………7分(Ⅱ)由(1)得
。
………………7分(Ⅱ)由(1)得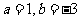 ,
,
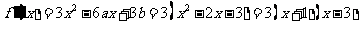 ………………9分
………………9分
令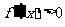 ,解得
,解得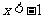 或
或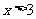 ;
………………10分令
;
………………10分令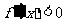 ,解得
,解得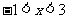 。 ………………12分于是当
。 ………………12分于是当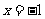 时,有极大值为
时,有极大值为
当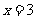 时,极小值为
时,极小值为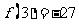 。
………………14分
。
………………14分
18、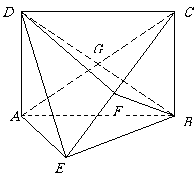 (本小题满分14分)
(本小题满分14分)
解:(Ⅰ)证明:如图6所示

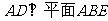 ,
,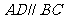
|
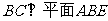 ,则
,则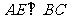 …………2分
…………2分
又
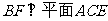 ,则
,则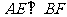
∴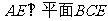 ………………4分
………………4分
(Ⅱ)证明:依题意可知: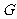 是
是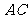 中点
中点

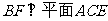 则
则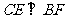 ,而
,而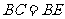
∴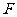 是
是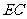 中点
………………6分
中点
………………6分
 在
在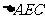 中,
中,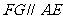
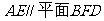 ………………8分
………………8分
(Ⅲ)
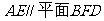
 ,而
,而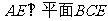 ……………… 9分
……………… 9分
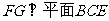 ,
,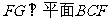 ………………10分
………………10分

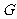 是
是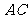 中点
中点
∴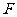 是
是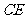 中点 ,
中点 ,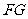
 且
且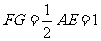 ………………11分
………………11分

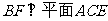
∴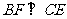 在
在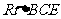 中,
中,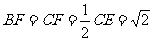 ………………12分
………………12分
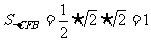 ……………… 13分
……………… 13分
 ………………14分
………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com