
12.在某一时期内。河流在这一处的年最高水位在各个范围的概率如下:
|
年最高水位 (单位:m) |
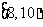 |
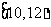 |
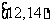 |
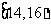 |
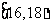 |
|
概率 |
0.1 |
0.28 |
0.38 |
0.16 |
0.08 |
那么在同一时期内,河流在这一处的最高水位在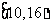 (m)的概率为
(m)的概率为
[点眼]某一范围内的概率等于其各区间内概率之和.
[解析]p=0.28+0.38+0.16=0.82.
11.

 二项式
二项式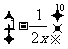 的展开式 中的中间项系数为
的展开式 中的中间项系数为
[点眼]n=10时,展开式共11项,中间项是第6项.
[解析]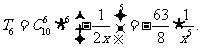 故所求系数为
故所求系数为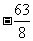 .
.
10.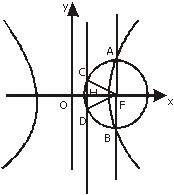 过双曲线
过双曲线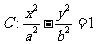 的右焦点F的直线
的右焦点F的直线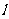 与双曲线右支相交于A,B两点,以线段AB为直径的圆被右准线截得的劣弧度数为
与双曲线右支相交于A,B两点,以线段AB为直径的圆被右准线截得的劣弧度数为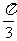 ,那么双曲线的离心率e=(
)
,那么双曲线的离心率e=(
)

[点眼]设弦AB的中点为M,圆M交右准线于C,D.则△MCD
必为等边三角形.当M,F重合时运算最为简洁.
|
得 .
.
此时圆半径 .如图4,当∠CFD=60°时,△CFD为正三角形.其边长为
.如图4,当∠CFD=60°时,△CFD为正三角形.其边长为 .设右准线交x轴于H,则
.设右准线交x轴于H,则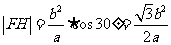 .
.
又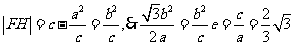 ,故选D.
,故选D.
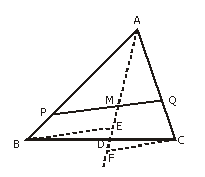
9.M为△ABC内一点,过点M的一直线交AB边于P,交AC边于Q,则
 条件p:“
条件p:“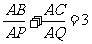 ”是条件q:“M是△ABC的重心” 成立的(
)
”是条件q:“M是△ABC的重心” 成立的(
)
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分又不必要条件.
[点眼]三角形的重心唯一,且分每条中线为2:1的两段.
[解析]如图3,连AM,并延长AM交BC于D.
作BE∥PQ,交直线AD于E,作CF∥PQ,交直线AD于F.那么:
|
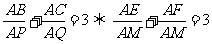
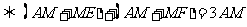
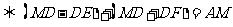
当且仅当DE=DF时,△BDE≌△CDF.此时BD=CD,即AD为△ABC中BC边的中线,且满足AM:MD=1:2.
∵条件p不一定满足DE=DF,∴p不是q成立的充分条件.但若q成立,则必有DE=DF,则p必定成立,
∴p是q成立的必要条件.故选B.
说明:我们在网上看到本题的标准答案是C(充分必要条件).这明显是错误的.例如在图3中,我们让点M在线段PQ上左右移动时,并不影响条件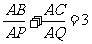 的成立.不可能由此得出线段PQ上的点都是△ABC的重心.至于错误的原因,到底是命题人的疏忽,还是技术方面的因素,则有待查证.
的成立.不可能由此得出线段PQ上的点都是△ABC的重心.至于错误的原因,到底是命题人的疏忽,还是技术方面的因素,则有待查证.
8.若函数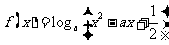 有最小值,则实数
有最小值,则实数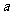 的取值范围是(
)
的取值范围是(
)

[点眼]设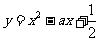 ,若a>1,则当函数y取最小值时f(x)也取得最小;当0<a<1时,y取最大值时f(x)才有最小.也就是说,本题题眼在复合函数的单调性.
,若a>1,则当函数y取最小值时f(x)也取得最小;当0<a<1时,y取最大值时f(x)才有最小.也就是说,本题题眼在复合函数的单调性.
[解析]根据对数函数的定义,显然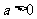 .且
.且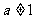 .
.
又由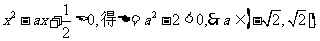 综合知:
综合知: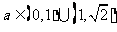 .排除D.
.排除D.
若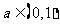 ,则
,则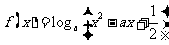 是其定义域上的减函数,∵函数
是其定义域上的减函数,∵函数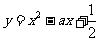 只有最小值,从而
只有最小值,从而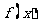 只有最大值,排除A,B故选C.
只有最大值,排除A,B故选C.
7.用0,1,2,3,4,5,6这6个数字组成无重复数字的三位数中能被9整除的个数为( )
A.14 B.16 C.18 D.24
[点眼]各位数字之和是9的倍数的整数一定能被9整除.
[解析]符合条件的三位数有且仅有以下3种情况:
由1,3,5组成的三维数能够被9整除,这样的三位数有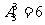 个;
个;
由2,3,4组成的三维数能够被9整除,这样的三位数也有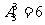 个;
个;
由0,4,5组成的三维数能够被9整除,这样的三位数也有 个.
个.
以上共计16个,选B.
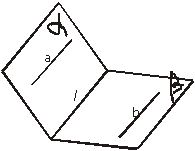
5.若a,b是异面直线,αβ是两个不同的平面,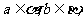
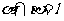 ,则(
)
,则(
)
A.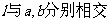 B.
B.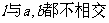
C.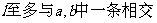 D.
D. 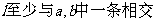
 [点眼]
[点眼]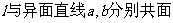
[解析]如图2,假定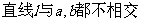 ,∵
,∵ 共面,
共面,
必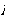 ∥
∥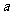 ,同理
,同理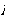 ∥
∥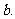 故
故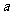 ∥
∥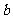 .这与
.这与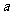 ,
,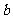 是异面直线矛盾.
是异面直线矛盾.
∴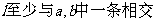 ,选D.
,选D.
|
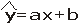 6.线性回归方程
必过点(
)
6.线性回归方程
必过点(
)

[点眼]线性回归方程是由散点变量的平均数归纳出来的.
[解析]散点变量的平均数一定适合线性回归方程,故选D.
4.飞机从甲地以北偏西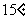 的方向飞行1400公里到达乙地,再从乙地以南偏东
的方向飞行1400公里到达乙地,再从乙地以南偏东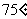 的方向飞行1400公里到达丙地,那么丙地距甲地距离为(
)
的方向飞行1400公里到达丙地,那么丙地距甲地距离为(
)
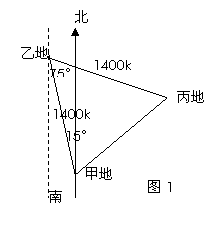

[点眼]甲、乙、丙三地连成等边三角形.
[解析]如图1,乙地与甲地、丙地等距离,且夹角为
60°,故丙地与甲地距离亦为1400km,选A.
3.函数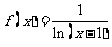 的反函数为(
)
的反函数为(
)
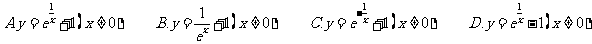
[点眼]互为反函数的两函数,定义域与值域互易,对应法则互逆
[解析]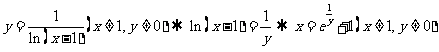
故所求反函数为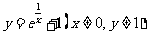 ,故选A.
,故选A.
2.已知等差数列 前n项和为
前n项和为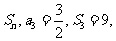 则
则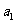 =(
)
=(
)

[点眼]已知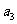 ,只要求出
,只要求出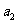 ,则
,则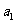 自动浮出.
自动浮出.
[解析]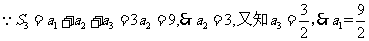 ,故选B.
,故选B.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com