
19、(本小题满分14分)
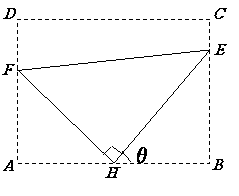
如图:某污水处理厂要在一个矩形污水处理池 的池底水平铺设污水净化管道
的池底水平铺设污水净化管道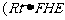 ,
,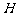 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口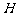 是
是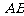 的中点,
的中点,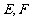 分别落在线段
分别落在线段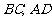 上.已知
上.已知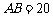 米,
米,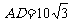 米,记
米,记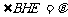 .
.
 (1)试将污水净化管道的长度
(1)试将污水净化管道的长度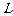 表示为
表示为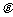 的函数,并写出定义域;
的函数,并写出定义域;
(2)若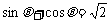 ,求此时管道的长度
,求此时管道的长度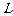 ;
;
(3)问:当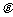 取何值时,污水净化效果最好?并求出此时
取何值时,污水净化效果最好?并求出此时
管道的长度.
答案1、解:(1)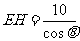 ,
,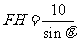 …………2分
…………2分
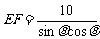 ……………………………………………………4分
……………………………………………………4分
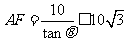
由于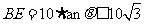 ,
,
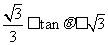 ,
, 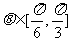 …………………………………………………5分
…………………………………………………5分
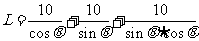 ,
, 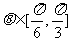 .……………………………6分
.……………………………6分
(2) 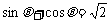 时,
时,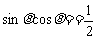 ,………………………………………7分
,………………………………………7分
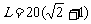 ;……………………………………………………………………8分
;……………………………………………………………………8分
(3)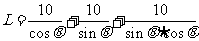 =
=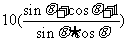
设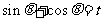 则
则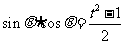 ……………………………………10分
……………………………………10分
由于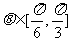 ,所以
,所以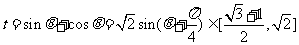 …12分
…12分
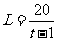 在
在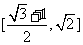 内单调递减,于是当
内单调递减,于是当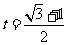 时
时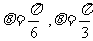 时
时
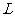 的最大值
的最大值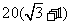 米. ………………………………………………………13分
米. ………………………………………………………13分
答:当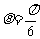 或
或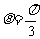 时所铺设的管道最短,为
时所铺设的管道最短,为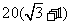 米.………………14分
米.………………14分
18、(本小题满分14分)
设平面内有四个向量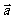 、
、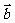 、
、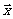 、
、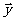 ,且满足
,且满足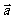 =
=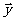 -
-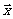 ,
,
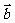 =2
=2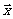 -
-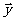 ,
,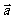 ⊥
⊥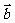 , |
, |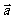 |=|
|=|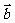 |=1
|=1
(1)求|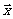 |,|
|,|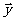 |;
|;
(2)若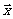 、
、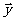 的夹角为
的夹角为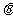 ,求cos
,求cos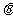 .
.
解:(1)
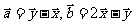
|
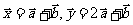
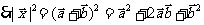
|
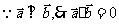

|
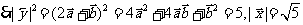
|
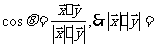
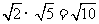
|
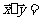
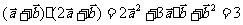
|
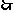
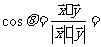
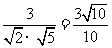
17、(本小题满分14分)
已知函数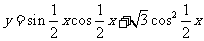 +1,求:
+1,求:
(1)求函数的单调减区间;
(2)求函数的最大值,以及函数取得最大值时自变量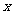 的集合
的集合
解:(1)将函数化简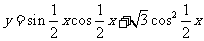 +1=
+1=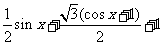
|
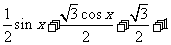 =
=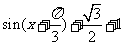
|
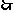 当
当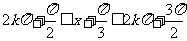 时,即
时,即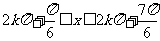
|
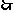 函数的单调减区间为
函数的单调减区间为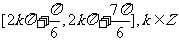 。
。
|
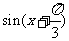 =1时,函数取得最大值为
=1时,函数取得最大值为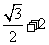 ,
,
此时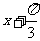 =
=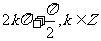
|
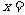
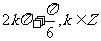 ,
,
|
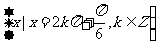
16、(本小题满分12分)
已知函数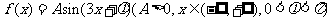 在
在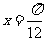 时取得最大值4。
时取得最大值4。
(1)求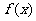 的最小正周期;
的最小正周期;
(2)求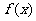 的解析式;
的解析式;
|
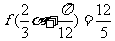 ,求
,求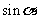 。
。
|
|
|
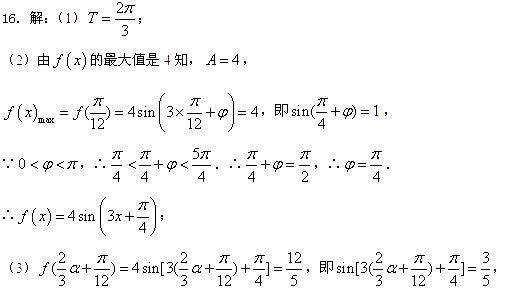
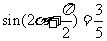 ,
,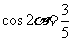 ,
,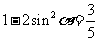 ,
,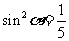 ,
,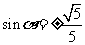 .
.
15、(本小题满分12分)已知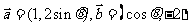 ,且
,且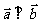
(1)求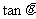 的值
的值
(2)求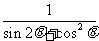 的值
的值
解:(1)由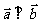 ,得
,得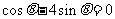 ,又
,又
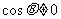 ,
,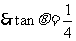 ……6分
……6分
(2)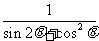 =
=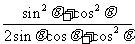 =
=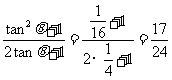 ……12分
……12分
14、已知函数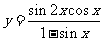 的值域为____
的值域为____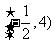 ______
______
13.给出下列命题:
①存在实数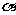 ,使
,使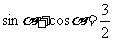
②函数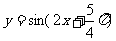 +1的一个对称中心为
+1的一个对称中心为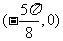
③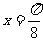 是函数
是函数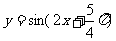 的一条对称轴方程
的一条对称轴方程
④若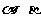 是第一象限的角,且
是第一象限的角,且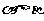 ,则
,则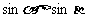
其中正确命题的序号是__________③___________
12、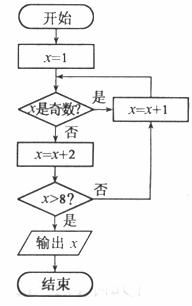 如图所示,程序框图(算法流程图)的输出值
如图所示,程序框图(算法流程图)的输出值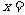 ____12____。
____12____。
11、以点(2,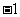 )为圆心且与直线
)为圆心且与直线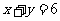 相切的圆的方程是
相切的圆的方程是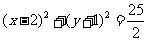
10.已知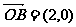 ,
,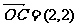 ,
,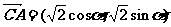
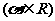 ,其中O为原点,则
,其中O为原点,则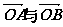 夹角的范围为
( D )
夹角的范围为
( D )
A.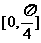 B.
B. 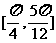 C.
C. 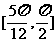 D .
D .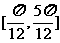
第Ⅱ卷(非选择题 共80分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com