
3.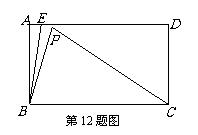 (2010山东济南)如图所示,矩形ABCD中,AB=4,BC=
(2010山东济南)如图所示,矩形ABCD中,AB=4,BC=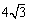 ,点E是折线段A-D-C上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有
,点E是折线段A-D-C上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有
A.2个 B.3个 C.4个 D.5个
答案:C
2.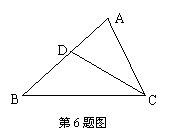 (2010山东济南)如图,在△ABC中,CD是∠ACB的平分线,∠A = 80°,∠ACB=60°,那么∠BDC=( )
(2010山东济南)如图,在△ABC中,CD是∠ACB的平分线,∠A = 80°,∠ACB=60°,那么∠BDC=( )
A.80° B.90°
C.100° D.110°
答案:D
1.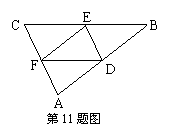 (2010昆明)如图,在△ABC中,点D、E、F分别是AB、BC、CA的中点,
(2010昆明)如图,在△ABC中,点D、E、F分别是AB、BC、CA的中点,
若△ABC的周长为10 cm,则△DEF的周长是 cm.
答案:5
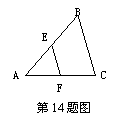
4.(2010黄冈)如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )B
A.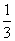 B.
B.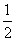 C.
C.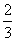 D.不能确定
D.不能确定

第15题图
3.(2010宁德)(本题满分8分)如图,已知AD是△ABC的角平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,需添加一个条件是:_______________,并给予证明.
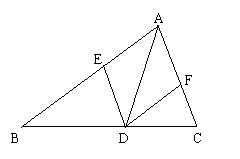
解法一:添加条件:AE=AF,………………3分
证明:在△AED与△AFD中,
∵AE=AF,∠EAD=∠FAD,AD=AD,………………6分
∴△AED≌△AFD(SAS). ………………8分
解法二:添加条件:∠EDA=∠FDA,………………3分
证明:在△AED与△AFD中,
∵∠EAD=∠FAD,AD=AD,∠EDA=∠FDA,………………6分
∴△AED≌△AFD(ASA). ………………8分
2. (2010宁德)如图,在△ABC中,点E、F分别为AB、AC的中点.
(2010宁德)如图,在△ABC中,点E、F分别为AB、AC的中点.
若EF的长为2,则BC的长为___________.4
1.(2010宁德)如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个
直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长是( ).B

A.2+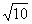 B.2+2
B.2+2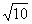 C.12 D.18
C.12 D.18
1、如图,已知点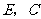 在线段
在线段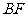 上,
上,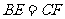 ,请在下列四个等式中,
,请在下列四个等式中,
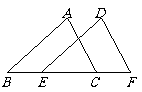 ①AB=DE,②∠ACB=∠F,③∠A=∠D,④AC=DF.选出两个作为条件,推出
①AB=DE,②∠ACB=∠F,③∠A=∠D,④AC=DF.选出两个作为条件,推出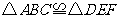 .并予以证明.(写出一种即可)
.并予以证明.(写出一种即可)
已知: , .
求证: .
.
证明:
答案: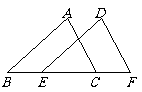 解:已知:①④(或②③、或②④)
解:已知:①④(或②③、或②④)
证明:若选①④
∵
∴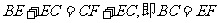 .
.
在△ABC和△DEF中
AB=DE,BC=EF,AC=DF.
∴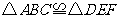 .
.
(选择②③、或②④评分标准类似,证明略)
(2010年天津市)(13)如图,已知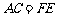 ,
,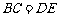 ,
,
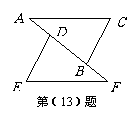 点A、D、B、F在一
点A、D、B、F在一
条直线上,要使△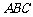 ≌△
≌△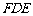 ,还需添加
,还需添加
一个条件,这个条件可以是
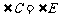
(答案不惟一,也可以是 或
或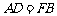 ) .
) .
(2010山西9.现有四根木棒,长度分别为4cm,6cm,8cm,10cm.从中任取一根木棒,能组成三角形的个数为()C
A.1个 B.2个 C.3个 D.4个
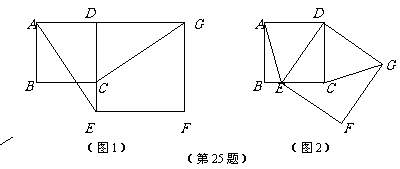
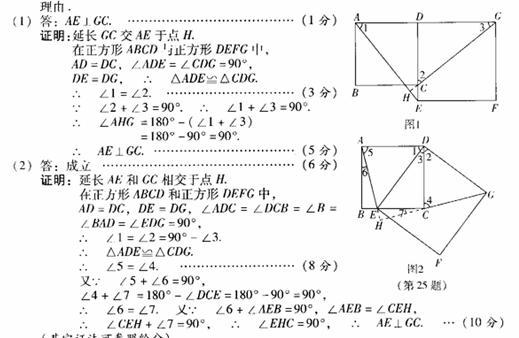
(2010山西25.(本题10分)如图1,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE、GC.
(1)试猜想AE与GC有怎样的位置关系,并证明你的结论.
(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图2,连接AE和CG。你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.

24.全等、四边形、勾股定理(10重庆潼南县)如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连结AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4.
(1)证明:△ABE≌△DAF;
(2)若∠AGB=30°,求EF的长.
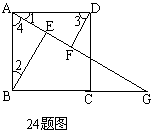

解:(1)∵四边形ABCD是正方形,∴AB=AD。
在△ABE和△DAF中,

∴△ABE≌△DAF。
(2)∵四边形ABCD是正方形,∴∠1+∠4=900。
∵∠3=∠4,∴∠1+∠3=900。∴∠AFD=900。
在正方形ABCD中,AD∥BC,∴∠1=∠AGB=300。
在Rt△ADF中,∠AFD=900,AD=2,∴AF=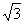 ,DF =1。
,DF =1。
由(1)得△ABE≌△ADF。∴AE=DF=1。∴EF=AF-AE=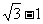 。
。
19.(10重庆潼南县)画一个等腰△ABC,使底边长BC=a,底边上的高为h(要求:用尺规作图,保留作图痕迹,写出已知,求作,不写作法和证明).
已知:
求作:
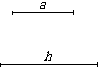

已知:线段a、h
求作:一个等腰△ABC使底边BC=a,底边BC上的高为h。-------------1分
画图(保留作图痕迹图略)--------------------------6分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com