
2.
函数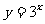 与
与 的图象关于下列那种图形对称( )
的图象关于下列那种图形对称( )
A. 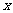 轴 B.
轴 B. 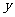 轴 C. 直线
轴 C. 直线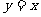 D. 原点中心对称
D. 原点中心对称
1. 下列函数与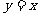 有相同图象的一个函数是( )
有相同图象的一个函数是( )
A. 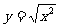 B.
B. 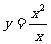
C. 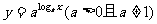 D.
D. 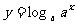
(四)巩固练习:
1.已知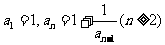 ,则
,则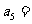
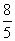 .
.
2.在数列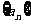 中
中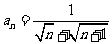 ,且
,且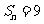 ,则
,则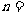
 .
.
(三)例题分析:
例1. 求下面各数列的一个通项:
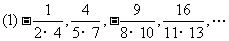 ;
;
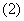 数列的前
数列的前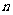 项的和
项的和 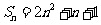 ;
;
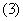 数列
数列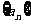 的前
的前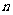 项和
项和 为不等于
为不等于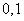 的常数) .
的常数) .
解:(1)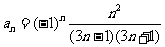 .
.
(2)当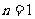 时
时
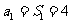 ,
当
,
当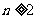 时
时
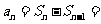
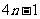 ,显然
,显然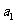 不适合
不适合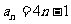
∴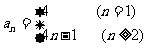 .
.
(3)由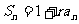 可得当
可得当 时
时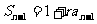 ,
,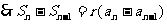 ,
,
∴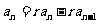 ,∴
,∴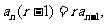 ∵
∵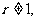 ∴
∴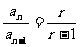 ,∵
,∵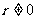 ,
,
∴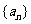 是公比为
是公比为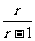 的等比数列.
的等比数列.
又当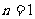 时,
时,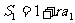 ,∴
,∴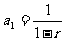 ,∴
,∴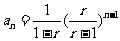 .
.
说明:本例关键是利用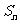 与
与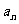 的关系进行转化.
的关系进行转化.
例2.根据下面各个数列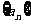 的首项和递推关系,求其通项公式:
的首项和递推关系,求其通项公式:
(1)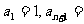
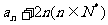 ;
;
(2)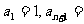
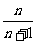
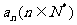 ;
;
(3)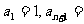
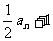
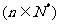 .
.
解:(1)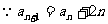 ,∴
,∴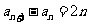 ,
,
∴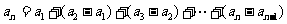
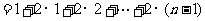
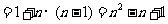
(2)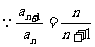 ,∴
,∴
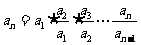 =
=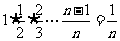 .
.
又解:由题意,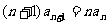 对一切自然数
对一切自然数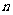 成立,
成立,
∴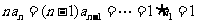 ,∴
,∴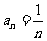 .
.
(3) 是首项为
是首项为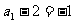
公比为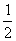 的等比数列,
的等比数列,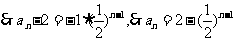 .
.
说明:(1)本例复习求通项公式的几种方法:迭加法、迭乘法、构造法;
(2)若数列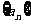 满足
满足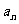
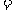
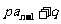 ,则数列
,则数列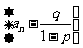 是公比为
是公比为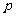 的等比数列.
的等比数列.
例3.设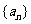 是正数组成的数列,其前
是正数组成的数列,其前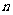 项和为
项和为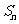 ,并且对所有自然数
,并且对所有自然数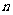 ,
,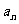 与
与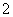 的等差中项等于
的等差中项等于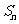 与
与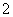 的等比中项,
的等比中项,
 写出数列
写出数列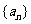 的前三项;
的前三项;  求数列
求数列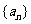 的通项公式(写出推证过程);
的通项公式(写出推证过程);
 令
令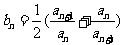
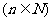 ,求
,求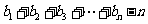 .
.
解:(1)由题意: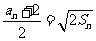
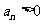 ,令
,令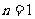 ,
,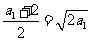 ,解得
,解得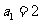
令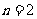 ,
,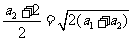 , 解得
, 解得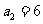
令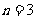 ,
,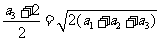 , 解得
, 解得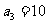
∴该数列的前三项为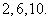
(2)∵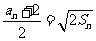 ,∴
,∴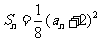 ,由此
,由此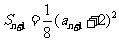 ,
,
∴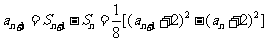 ,整理得:
,整理得: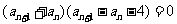
由题意: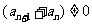 ,∴
,∴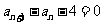 ,即
,即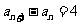 ,
,
∴数列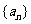 为等差数列,其中
为等差数列,其中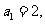 公差
公差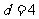 ,
, ∴
∴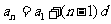
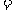

(3)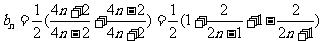
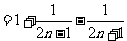
∴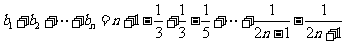

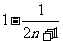 .
.
例4.(《高考 计划》考点19“智能训练第17题”)
计划》考点19“智能训练第17题”)
设函数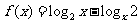
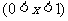 ,数列
,数列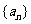 满足
满足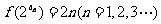
(1)求数列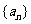 的通项公式; (2)判定数列
的通项公式; (2)判定数列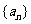 的单调性.
的单调性.
解答参看《高考 计划》教师用书
计划》教师用书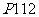 .
.
(二)主要方法:
1.给出数列的前几项,求通项时,要对项的特征进行认真的分析、化归;
2.数列前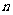 项的和
项的和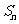 和通项
和通项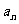 是数列中两个重要的量,在运用它们的关系式
是数列中两个重要的量,在运用它们的关系式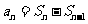 时,一定要注意条件
时,一定要注意条件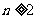 ,求通项时一定要验证
,求通项时一定要验证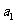 是否适合.
是否适合.
(一)主要知识:
1.数列的有关概念;
2.数列的表示方法:(1)列举法;(2)图象法;(3)解析法;(4)递推法.
3.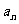 与
与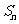 的关系:
的关系: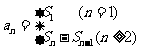 .
.
3.从你熟悉的树(比如松树、柳树……)中选一种,描绘它的形象,阐述它的象征意义。文辞要优美。(8分)
答:
焦作市2009-2010学年(下)《中国现代诗歌散文欣赏》水平测试
2.方文山的歌词“你发如雪,凄美了离别”中的“凄美”本来是形容词,在这里转变成动词使用。请你从熟悉的现代诗歌或歌词中再举两个词类活用的例子加以说明。(6分)
答:
1.舒婷《神女峰》中的著名诗句“与其在悬崖上展览千年/不如在爱人肩头痛哭一晚”中的“展览”能否换成“展望”?请结合全诗谈谈你的看法。(6分)
答:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com