
3.能利用二项式定理求近似值,证明整除问题,证明不等式.
2.能熟练地逆向运用二项式定理求和.
1.能利用二项式系数的性质求多项式系数的和与求一些组合数的和.
19.设数列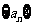 和
和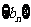 满足
满足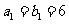 ,
,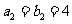 ,
,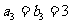 ,且数列
,且数列

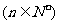 是等差数列,数列
是等差数列,数列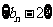
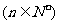 是等比数列。
是等比数列。
(Ⅰ)求数列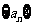 和
和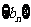 的通项公式;
的通项公式;
(Ⅱ)是否存在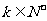 ,使
,使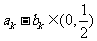 ?若存在,求出
?若存在,求出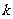 的值;若不存在,说明理由。
的值;若不存在,说明理由。
18.已知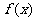 在
在 上是增函数,而且
上是增函数,而且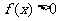 ,
,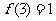 。判断
。判断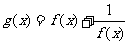
在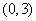 上是增函数还是减函数,并加以证明。
上是增函数还是减函数,并加以证明。
解:函数g(x)在 (0,3)上是减函数. 证明如下:任取0<x1<x2≤3,
则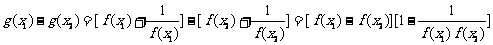 .
.
∵f(x)在(0,+∞)是增函数,∴f(x1)-f(x2)<0. 又f(x)>0,f(3)=1,
∴0<f(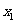 )<f(
)<f(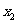 )≤f(3)=1,
)≤f(3)=1,
∴0<f(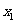 )·f(
)·f(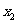 )<1,
)<1,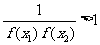 ,
,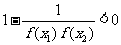 .
.
∴g(x1)- g(x2)>0,即g(x1) >g(x2)
由此可知,函数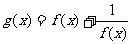 在(0,3)上是减函数。
在(0,3)上是减函数。
17.已知: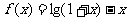 在
在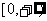 上是减函数,解关于
上是减函数,解关于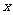 的不等式
的不等式
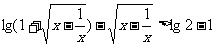 .
.
解:由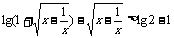 ,得
,得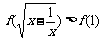 .
.

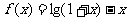 在
在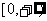 上是减函数,
上是减函数, 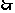
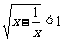 ,这等价于
,这等价于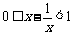 ,
,
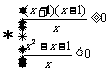 ,解之得
,解之得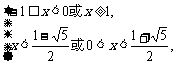
故不等式的解为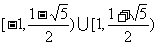 .
.
16.数列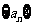 中,
中,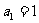 ,当
,当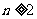 时,其前
时,其前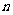 项和
项和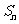 满足
满足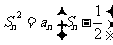 。
。
(Ⅰ)求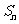 的表达式;
的表达式;
(Ⅱ)设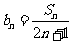 ,数列
,数列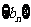 的前
的前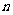 项和为
项和为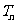 ,求
,求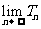 。
。
15.已知数列|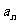 |满足
|满足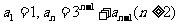
(I)求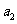 ,
,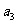 ;
;
(II)证明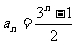 。
。
14.若干个能唯一确定一个数列的量称为该数列的“基本量”。设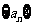 是公比为
是公比为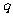 的无穷等比数列,下列
的无穷等比数列,下列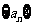 的四组量中,一定能成为该数列“基本量”的是第
① ④ 组。(写出所有符合要求的组号)
的四组量中,一定能成为该数列“基本量”的是第
① ④ 组。(写出所有符合要求的组号)
①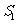 与
与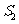 ; ②
; ②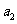 与
与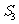 ; ③
; ③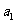 与
与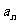 ; ④
; ④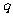 与
与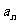
其中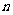 为大于
为大于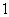 的整数,
的整数,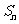 为
为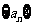 的前
的前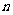 项和。
项和。
13.某航空公司规定,乘机所携带行李的重量(kg)与其运费(元)由如图的一次函数图像确定,那么乘客免费可携带行李的最大重量为____________;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com