
16.(本小题满分12分)已知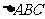 中,
中,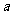 、
、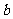 、
、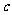 是三个内角
是三个内角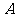 、
、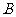 、
、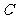 的对边,关于
的对边,关于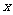 的不等式
的不等式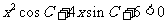 的解集是空集.
的解集是空集.
(1)求角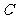 的最大值;
的最大值;
(2)若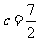 ,
,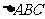 的面积
的面积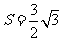 ,求当角
,求当角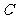 取最大值时
取最大值时 的值.
的值.
15.设函数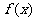 的定义域为D,若存在非零实数
的定义域为D,若存在非零实数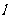 使得对于任意
使得对于任意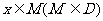 ,有
,有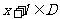 ,且
,且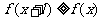 ,则称
,则称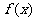 为M上的
为M上的 高调函数。
高调函数。
如果定义域为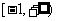 的函数
的函数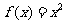 为
为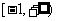 上的
上的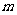 高调函数,那么实数
高调函数,那么实数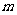 的取值范围是
。如果定义域为R的函数
的取值范围是
。如果定义域为R的函数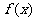 是奇函数,当
是奇函数,当 时,
时,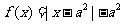 ,且
,且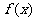 为R上的4高调函数,那么实数
为R上的4高调函数,那么实数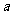 的取值范围是 。
的取值范围是 。
14.实数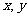 满足
满足 ,目标函数
,目标函数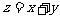 ,则当
,则当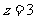 时,
时,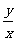 的取值范围是
.
的取值范围是
.
13.在等比数列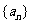 中,若
中,若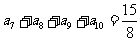 ,
,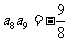 ,则
,则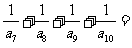
。
12.已知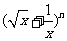
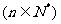 展开式中常数项是
展开式中常数项是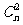 ,则
,则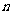 的值为
.
的值为
.
11.已知向量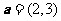 ,
,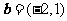 ,则
,则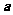 在
在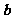 方向上的投影等于
.
方向上的投影等于
.
10.已知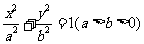 ,
,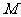 、
、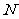 是椭圆上关于原点对称的两点,
是椭圆上关于原点对称的两点,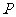 是椭圆上任意一点,且直线
是椭圆上任意一点,且直线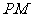 、
、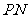 的斜率分别为
的斜率分别为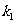 、
、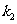 (
(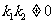 ),若
),若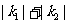 的最小值为1,则椭圆的离心率为(
)
的最小值为1,则椭圆的离心率为(
)
A.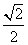 B.
B. 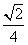 C.
C.
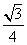 D.
D.
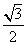
9.现有四所大学进行自主招生,同时向一所高中的已获省级竞赛一等奖的甲、乙、丙、丁四位学生发出录取通知书.若这四名学生都愿意进这四所大学的任意一所就读, 则仅有两名学生被录取到同一所大学的概率为( )
A.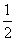 B.
B.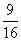 C.
C.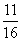 D.
D.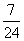
8.对于函数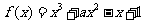 的极值情况,4位同学有下列说法:
的极值情况,4位同学有下列说法:
甲:该函数必有2个极值;
乙:该函数的极大值必大于1;
丙:该函数的极小值必小于1;
丁:方程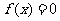 一定有三个不等的实数根。
一定有三个不等的实数根。
这四种说法中,正确的个数是( )
A.1个 B.2个 C.3个 D.4个
7.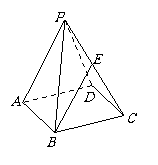 如图在棱长均为2的正四棱锥P-ABCD中,点E为PC中点,则下列命题正确的是( )
如图在棱长均为2的正四棱锥P-ABCD中,点E为PC中点,则下列命题正确的是( )
A.BE∥面PAD,且直线BE到面PAD距离为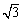
B.BE∥面PAD,且直线BE到面PAD距离为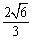
C.BE不平行于面PAD,且BE与平面PAD所成角大于30°
D.BE不平行于面PAD,且BE与面PAD所成角小于30°
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com