
24.选修4-5;不等式选讲
设|a|<1,函数f(x)=ax2+x-a(-1≤x≤1),证明:|f(x)|≤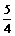
宁夏银川一中2010届高三下学期第二次模拟考试
23.选修4-4:坐标系与参数方程
在抛物线y2=4a(x+a)(a>0),设有过原点O作一直线分别
交抛物线于A、B两点,如图所示,试求|OA|•|OB|的最小值。
请考生在第22、23、24题中任选一题做答,如果多做,则按所
做的第一题记分.做答时,用2B铅笔在答题卡上把所选题目对应的
题号涂黑.
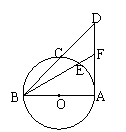
22.选修4-1:几何证明选讲
如图,BA是⊙O的直径,AD是切线,BF、BD是割线,
求证:BE•BF=BC•BD
21.(本小题满分12分)
设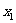 、
、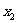
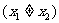 是函数
是函数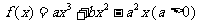 的两个极值点。
的两个极值点。
(1)若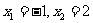 ,求函数
,求函数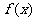 的解析式;
的解析式;
(2)若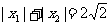 ,求
,求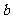 的最大值。
的最大值。
(3)若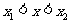 ,且
,且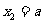 ,
,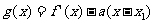 ,求证:
,求证: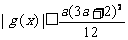 。
。
20.(本小题满分12分)
设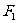 、
、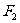 分别是椭圆
分别是椭圆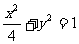 的左、右焦点.
的左、右焦点.
(1)若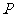 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求
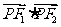 的取值范围;
的取值范围;
(2)设过定点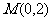 的直线
的直线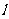 与椭圆交于不同的两点M、N,且∠
与椭圆交于不同的两点M、N,且∠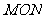 为锐角(其中
为锐角(其中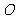 为坐标原点),求直线
为坐标原点),求直线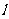 的斜率
的斜率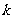 的取值范围.
的取值范围.
(3)设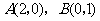 是它的两个顶点,直线
是它的两个顶点,直线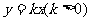 与AB相交于点D,与椭圆相交于E、F两点.求四边形
与AB相交于点D,与椭圆相交于E、F两点.求四边形 面积的最大值.
面积的最大值.
19.(本小题满分12分)
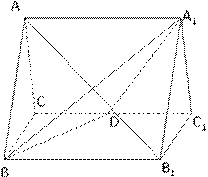 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,
D为CC1中点。
(1)求证:AB1⊥面A1BD;
(2)求二面角A-A1D-B的正弦值;
18.(本小题满分12分)
某单位为加强普法宣传力度,增强法律意识,举办了“普法知识竞赛”,现有甲、乙、丙三人同时回答一道有关法律知识的问题,已知甲回答对这道题的概率是 ,甲、丙两人都回答错误的概率是
,甲、丙两人都回答错误的概率是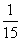 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是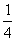 .
.
(1)求乙、丙两人各自回答对这道题的概率。
(2)求甲、乙、丙三人中恰有两人回答对该题的概率。
17.(本小题满分12分)
在数列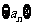 中,
中,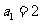 ,
,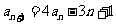 ,
,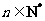 .
.
(1)证明数列 是等比数列;
是等比数列;
(2)设数列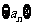 的前
的前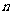 项和
项和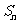 ,求
,求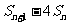 的最大值。
的最大值。
16.某公司计划在北京、上海、兰州、银川四个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该公司不同的投资方案种数是 (用数字作答).
15.如图ABC-A1B1C1是直三棱柱,∠BCA=90°,点E、F分别是A1B1、A1C1
的中点,若BC=CA=AA1,则BE与AF所成角的余弦值为__________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com