
243、不易之论:易,更改。完全正确,不可更改的言论。
242、不修边幅:边幅,本指布帛的边缘,比喻仪表、衣着、生活作风。原来形容为人不拘小节,后来形容不注意衣着、容貌的整洁。
241、不容置喙:置,安放; 喙,嘴。不许插嘴。
9.(本小题满分14分)
已知数列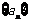 各项均不为0,其前
各项均不为0,其前 项和为
项和为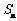 ,且对任意
,且对任意 都有
都有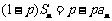 (
(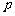 为大于1的常数),记
为大于1的常数),记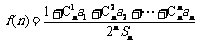 .
.
(1) 求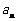 ;
;
(2) 试比较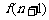 与
与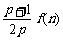 的大小(
的大小( );
);
(3) 求证: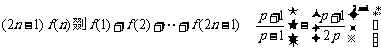 ,(
,( ).
).
解:(1) ∵ , ①
, ①
∴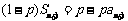 . ②
. ②
②-①,得
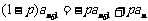 ,
,
即 . (3分)
. (3分)
在①中令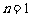 ,可得
,可得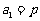 .
.
∴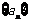 是首项为
是首项为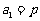 ,公比为
,公比为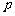 的等比数列,
的等比数列, . (4分)
. (4分)
(2) 由(1)可得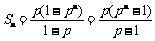 .
.

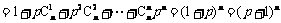 .
.
∴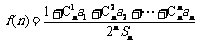
 , (5分)
, (5分)
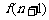
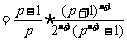 .
.
而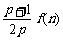
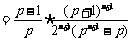 ,且
,且 ,
,
∴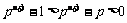 ,
,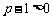 .
.
∴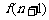

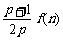 ,(
,( ). (8分)
). (8分)
(3) 由(2)知 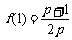 ,
,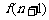

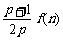 ,(
,( ).
).
∴当 时,
时, .
.
∴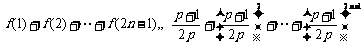
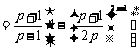 , (10分)
, (10分)
(当且仅当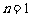 时取等号).
时取等号).
另一方面,当 ,
,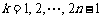 时,
时,

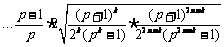
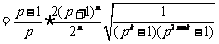
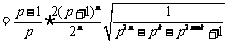 .
.
∵ ,∴
,∴ .
.
∴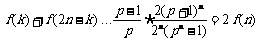 ,(当且仅当
,(当且仅当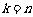 时取等号).(13分)
时取等号).(13分)
∴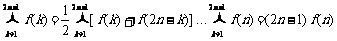 .(当且仅当
.(当且仅当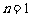 时取等号).
时取等号).
综上所述,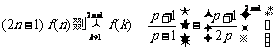 ,(
,( ).(14分)
).(14分)
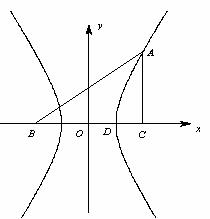
8.(本小题满分12分)
如图,直角坐标系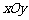 中,一直角三角形
中,一直角三角形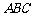 ,
,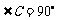 ,
, 、
、 在
在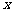 轴上且关于原点
轴上且关于原点 对称,
对称, 在边
在边 上,
上,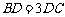 ,
,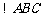 的周长为12.若一双曲线
的周长为12.若一双曲线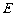 以
以 、
、 为焦点,且经过
为焦点,且经过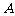 、
、 两点.
两点.

(1)求双曲线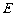 的方程;
的方程;
(2)若一过点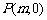 (
(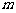 为非零常数)的直线
为非零常数)的直线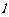 与双曲线
与双曲线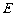 相交于不同于双曲线顶点的两点
相交于不同于双曲线顶点的两点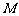 、
、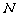 ,且
,且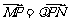 ,问在
,问在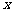 轴上是否存在定点
轴上是否存在定点 ,使
,使 ?若存在,求出所有这样定点
?若存在,求出所有这样定点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
解:(1) 设双曲线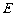 的方程为
的方程为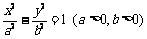 ,
,
则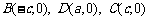 .
.
由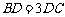 ,得
,得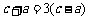 ,即
,即 .
.
∴ (3分)
(3分)
解之得 ,∴
,∴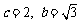 .
.
∴双曲线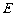 的方程为
的方程为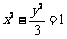 . (5分)
. (5分)
(2) 设在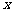 轴上存在定点
轴上存在定点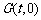 ,使
,使 .
.
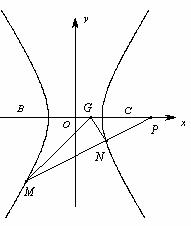
设直线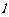 的方程为
的方程为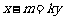 ,
,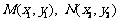 .
.
由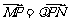 ,得
,得 .
.
即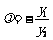 ① (6分)
① (6分)
∵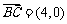 ,
,
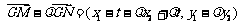 ,
,
∴
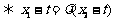 .
.
即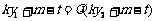 . ② (8分)
. ② (8分)
把①代入②,得
 ③ (9分)
③ (9分)
把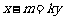 代入
代入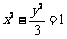 并整理得
并整理得
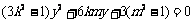
其中 且
且 ,即
,即 且
且 .
.
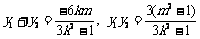 . (10分)
. (10分)
代入③,得
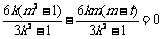 ,
,
化简得  .
.
当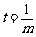 时,上式恒成立.
时,上式恒成立.
因此,在 轴上存在定点
轴上存在定点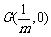 ,使
,使 . (12分)
. (12分)
7.(本小题满分14分)
设函数 在
在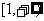 上是增函数.
上是增函数.
(1) 求正实数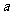 的取值范围;
的取值范围;
(2) 设 ,求证:
,求证:
解:(1)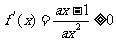 对
对 恒成立,
恒成立,
 对
对 恒成立
恒成立
又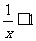
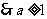 为所求.…………………………4分
为所求.…………………………4分
(2)取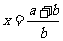 ,
,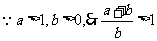 ,
,
一方面,由(1)知 在
在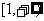 上是增函数,
上是增函数,
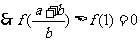

即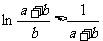 ……………………………………8分
……………………………………8分
另一方面,设函数
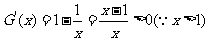
∴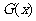 在
在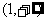 上是增函数且在
上是增函数且在 处连续,又
处连续,又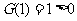
∴当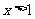 时,
时,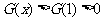
∴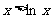 即
即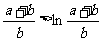
综上所述, ………………………………………………14分
………………………………………………14分
又MN⊥MQ,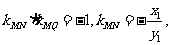 所以
所以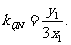
直线QN的方程为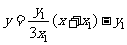 ,又直线PT的方程为
,又直线PT的方程为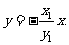 ……10分
……10分
从而得 所以
所以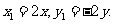
代入(1)可得 此即为所求的轨迹方程.………………13分
此即为所求的轨迹方程.………………13分
6.(本小题满分12分)
过抛物线 上不同两点A、B分别作抛物线的切线相交于P点,
上不同两点A、B分别作抛物线的切线相交于P点,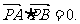
(1)求点P的轨迹方程;
(2)已知点F(0,1),是否存在实数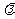 使得
使得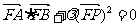 ?若存在,求出
?若存在,求出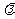 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
解法(一):(1)设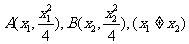
由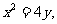 得:
得:
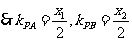
 ………………………………3分
………………………………3分
直线PA的方程是: 即
即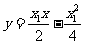 ①
①
同理,直线PB的方程是: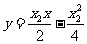 ②
②
由①②得: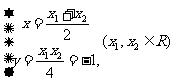
∴点P的轨迹方程是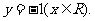 ……………………………………6分
……………………………………6分
(2)由(1)得: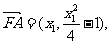
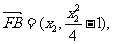
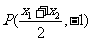
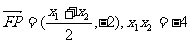
 …………………………10分
…………………………10分

所以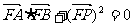
故存在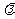 =1使得
=1使得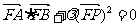 …………………………………………12分
…………………………………………12分
解法(二):(1)∵直线PA、PB与抛物线相切,且
∴直线PA、PB的斜率均存在且不为0,且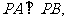
设PA的直线方程是
由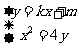 得:
得: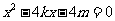
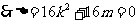 即
即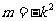 …………………………3分
…………………………3分
即直线PA的方程是: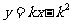
同理可得直线PB的方程是: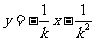
由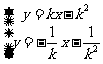 得:
得:
故点P的轨迹方程是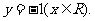 ……………………………………6分
……………………………………6分
(2)由(1)得: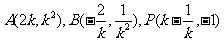
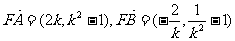
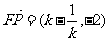
 ………………………………10分
………………………………10分

故存在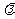 =1使得
=1使得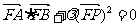 …………………………………………12分
…………………………………………12分
28.任选下面一题,按要求写作。(60分)
A.以“失败”为话题,自拟题目,写一篇不少于700字的议论文。
B.以《经典著作与快餐文化》为题,写一篇不少于700字的议论文。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com