
5.(本小题满分14分,第一小问满分4分,第二小问满分10分)
已知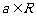 ,函数
,函数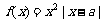 .
.
(Ⅰ)当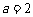 时,求使
时,求使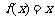 成立的
成立的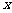 的集合;
的集合;
(Ⅱ)求函数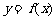 在区间
在区间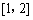 上的最小值.
上的最小值.
本小题主要考查运用导数研究函数性质的方法,考查分类讨论的数学思想和分析推理能力. 满分14分.
解:(Ⅰ)由题意,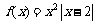 .
.
当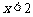 时,
时,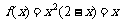 ,解得
,解得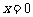 或
或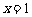 ;
;
当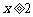 时,
时,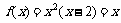 ,解得
,解得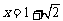 .
.
综上,所求解集为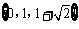 .
.
(Ⅱ)设此最小值为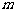 .
.
①当 时,在区间
时,在区间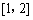 上,
上,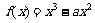 .
.
因为
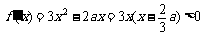 ,
,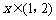 ,
,
则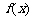 在区间
在区间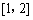 上是增函数,所以
上是增函数,所以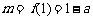 .
.
②当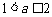 时,在区间
时,在区间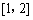 上,
上,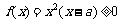 ,由
,由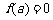 知
知
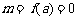 .
.
③当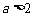 时,在区间
时,在区间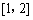 上,
上,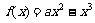 .
.
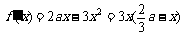 .
.
若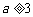 ,在区间
,在区间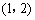 内
内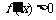 ,从而
,从而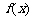 为区间
为区间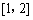 上的增函数,
上的增函数,
由此得
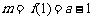 .
.
若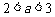 ,则
,则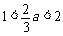 .
.
当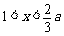 时,
时,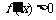 ,从而
,从而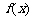 为区间
为区间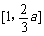 上的增函数;
上的增函数;
当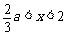 时,
时,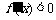 ,从而
,从而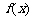 为区间
为区间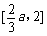 上的减函数.
上的减函数.
因此,当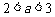 时,
时,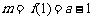 或
或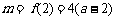 .
.
当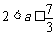 时,
时,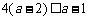 ,故
,故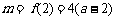 ;
;
当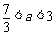 时,
时,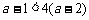 ,故
,故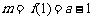 .
.
综上所述,所求函数的最小值

4.(本小题满分14分)
已知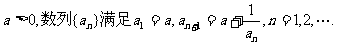
(I)已知数列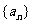 极限存在且大于零,求
极限存在且大于零,求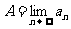 (将A用a表示);
(将A用a表示);
(II)设
(III)若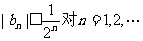 都成立,求a的取值范围.
都成立,求a的取值范围.
本小题主要考查数列、数列极限的概念和数学归纳法,考查灵活运用数学知识分析问题和解决问题的能力,满分14分.
解:(I)由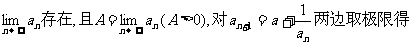
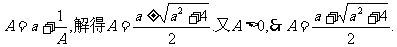
(II)
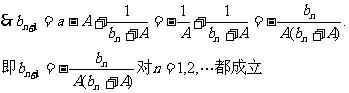
(III)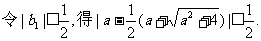

(i)当n=1时结论成立(已验证).
(ii)假设当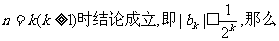

故只须证明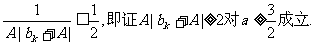
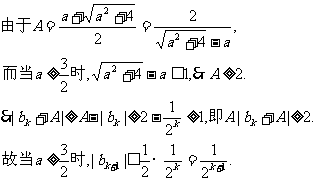
即n=k+1时结论成立.
根据(i)和(ii)可知结论对一切正整数都成立.
故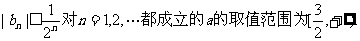
3.(本小题满分12分)
某突发事件,在不采取任何预防措施的情况下发生的概率为0.3,一旦发生,将造成400万元的损失. 现有甲、乙两种相互独立的预防措施可供采用. 单独采用甲、乙预防措施所需的费用分别为45万元和30万元,采用相应预防措施后此突发事件不发生的概率为0.9和0.85. 若预防方案允许甲、乙两种预防措施单独采用、联合采用或不采用,请确定预防方案使总费用最少.
(总费用=采取预防措施的费用+发生突发事件损失的期望值.)
本小题考查概率的基本知识和数学期望概念及应用概率知识解决实际问题的能力,满分12分.
解:①不采取预防措施时,总费用即损失期望为400×0.3=120(万元);
②若单独采取措施甲,则预防措施费用为45万元,发生突发事件的概率为
1-0.9=0.1,损失期望值为400×0.1=40(万元),所以总费用为45+40=85(万元)
③若单独采取预防措施乙,则预防措施费用为30万元,发生突发事件的概率为1-0.85=0.15,损失期望值为400×0.15=60(万元),所以总费用为30+60=90(万元);
④若联合采取甲、乙两种预防措施,则预防措施费用为45+30=75(万元),发生突发事件的概率为(1-0.9)(1-0.85)=0.015,损失期望值为400×0.015=6(万元),所以总费用为75+6=81(万元).
综合①、②、③、④,比较其总费用可知,应选择联合采取甲、乙两种预防措施,可使总费用最少.
2.(本小题满分12分)
如图,P是抛物线C:y=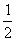 x2上一点,直线l过点P且与抛物线C交于另一点Q.
x2上一点,直线l过点P且与抛物线C交于另一点Q.
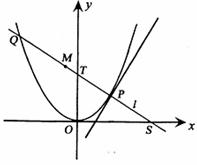
(Ⅰ)若直线l与过点P的切线垂直,求线段PQ中点M的轨迹方程;
(Ⅱ)若直线l不过原点且与x轴交于点S,与y轴交于点T,试求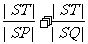 的取值范围.
的取值范围.
本题主要考查直线、抛物线、不等式等基础知识,求轨迹方程的方法,解析几何的基本思想和综合解题能力.满分12分.
解:(Ⅰ)设P(x1,y1),Q(x2,y2),M(x0,y0),依题意x1≠0,y1>0,y2>0.
由y=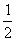 x2,
①
x2,
①
得y'=x.
∴过点P的切线的斜率k切= x1,
∴直线l的斜率kl=-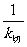 =-
=-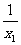 ,
,
∴直线l的方程为y-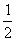 x12=-
x12=-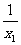 (x-x1),
(x-x1),
方法一:
联立①②消去y,得x2+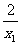 x-x12-2=0.
x-x12-2=0.
∵M是PQ的中点
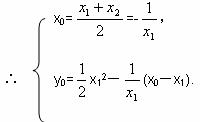
消去x1,得y0=x02+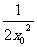 +1(x0≠0),
+1(x0≠0),
∴PQ中点M的轨迹方程为y=x2+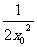 +1(x≠0).
+1(x≠0).
方法二:
由y1=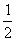 x12,y2=
x12,y2=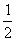 x22,x0=
x22,x0=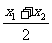 ,
,
得y1-y2=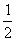 x12-
x12-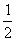 x22=
x22=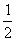 (x1+x2)(x1-x2)=x0(x1-x2),
(x1+x2)(x1-x2)=x0(x1-x2),
则x0=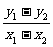 =kl=-
=kl=-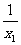 ,
,
∴x1=-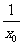 ,
,
将上式代入②并整理,得
y0=x02+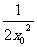 +1(x0≠0),
+1(x0≠0),
∴PQ中点M的轨迹方程为y=x2+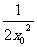 +1(x≠0).
+1(x≠0).
(Ⅱ)设直线l:y=kx+b,依题意k≠0,b≠0,则T(0,b).
分别过P、Q作PP'⊥x轴,QQ'⊥y轴,垂足分别为P'、Q',则
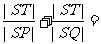
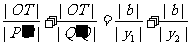 .
.
由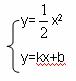 消去x,得y2-2(k2+b)y+b2=0. ③
消去x,得y2-2(k2+b)y+b2=0. ③
则 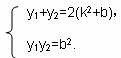
方法一:
∴ |b|(
|b|(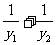 )≥2|b|
)≥2|b|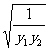 =2|b|
=2|b|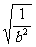 =2.
=2.
∵y1、y2可取一切不相等的正数,
∴ 的取值范围是(2,+
的取值范围是(2,+ ).
).
方法二:
∴ =|b|
=|b|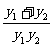 =|b|
=|b|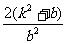 .
.
当b>0时, =b
=b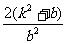 =
=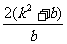 =
=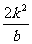 +2>2;
+2>2;
当b<0时, =-b
=-b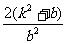 =
=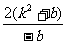 .
.
又由方程③有两个相异实根,得△=4(k2+b)2-4b2=4k2(k2+2b)>0,
于是k2+2b>0,即k2>-2b.
所以 >
>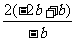 =2.
=2.
∵当b>0时,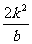 可取一切正数,
可取一切正数,
∴ 的取值范围是(2,+
的取值范围是(2,+ ).
).
方法三:
由P、Q、T三点共线得kTQ=KTP,
即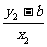 =
=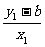 .
.
则x1y2-bx1=x2y1-bx2,即b(x2-x1)=(x2y1-x1y2).
于是b=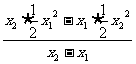 =-
=-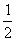 x1x2.
x1x2.
|
|
 =
=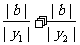 =
=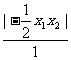 +
+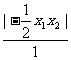 =
=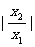 +
+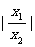 ≥2.
≥2.
∵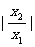 可取一切不等于1的正数,
可取一切不等于1的正数,
∴ 的取值范围是(2,+
的取值范围是(2,+ ).
).
1.(本小题满分14分)
已知f(x)=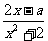 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值组成的集合A;
(Ⅱ)设关于x的方程f(x)=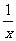 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
本小题主要考查函数的单调性,导数的应用和不等式等有关知识,考查数形结合及分类讨论思想和灵活运用数学知识分析问题和解决问题的能力.满分14分.
解:(Ⅰ)f'(x)=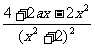 =
=
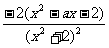 ,
,
∵f(x)在[-1,1]上是增函数,
∴f'(x)≥0对x∈[-1,1]恒成立,
即x2-ax-2≤0对x∈[-1,1]恒成立. ①
设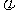 (x)=x2-ax-2,
(x)=x2-ax-2,
方法一:
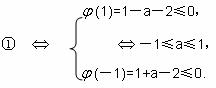
∵对x∈[-1,1],f(x)是连续函数,且只有当a=1时,f'(-1)=0以及当a=-1时,f'(1)=0
∴A={a|-1≤a≤1}. 方法二:
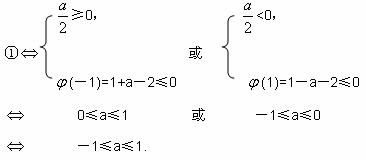
∵对x∈[-1,1],f(x)是连续函数,且只有当a=1时,f'(-1)=0以及当a=-1时,f'(1)=0
∴A={a|-1≤a≤1}.
(Ⅱ)由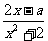 =
=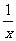 ,得x2-ax-2=0, ∵△=a2+8>0
,得x2-ax-2=0, ∵△=a2+8>0
∴x1,x2是方程x2-ax-2=0的两非零实根,
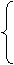 x1+x2=a,
x1+x2=a,
∴
从而|x1-x2|=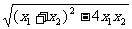 =
= .
.
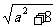
x1x2=-2,
∵-1≤a≤1,∴|x1-x2|= ≤3.
≤3.
要使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,
当且仅当m2+tm+1≥3对任意t∈[-1,1]恒成立,
即m2+tm-2≥0对任意t∈[-1,1]恒成立. ②
设g(t)=m2+tm-2=mt+(m2-2),
方法一:
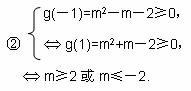
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
方法二:
当m=0时,②显然不成立;
当m≠0时,
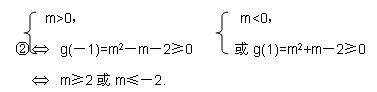
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
17.阅渎下面两则材料,回答问题。(10分)
材料一:今年,在深圳的不少茶馆或者素食馆,每天都有一群传统国学爱好者自发地聚集在一起,听专家讲解《弟子规》《增广贤丈》等国学经典。深圳还有一部分企业家,出钱出力组织员工一起学国学,把国学修养作为考核员工的重要标准。
材料二:早在1998年,广州市五一小学就试行“读经”;湖北武汉大学早在4年前就创办了国学试验班。发展至今,中国大陆有l00多个城市的800万孩子加入“读经”行列。
(1)用一句话概括以上材料的内容。(2分)
(2)你对上述现象有何看法?请简要阐述理由。(150字左右)(8分)
16.请根据下面曲线图回答问题。
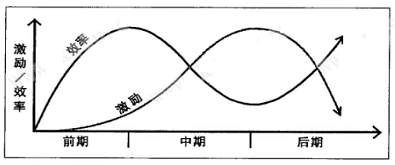
[注]深色曲线表示团队的工作效率,浅色曲线表示激励力度。
(1)团队的工作效率与激励力度之间的关系是:在工作前期,团队的工作效率呈上升趋势,激励力度逐渐加大;当丁作进行到中期时, ;当工作进行到后期时,团队的工作效率再次呈上升趋势,激励力度逐步降低。
(2)上图所反映的工作效率与激励力度变化的规律,给领导者的启示是:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com