
+[200÷30]=146
(式中[x]为不超过x的最大整数)
所以,符合条件的数共有200-146=54(个)
[例1]已知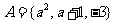 ,
,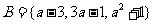 若
若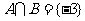 ,求实数a的值。
,求实数a的值。
解:由已知: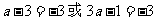
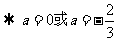
检验: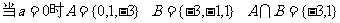
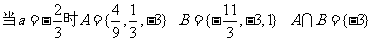
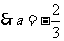
温馨提示:注意回代检验。
[例2]已知非空集合M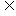 {1,2,3,4,5,6,7,8,9},且若a∈M,则10-a∈M,求集合M的个数
{1,2,3,4,5,6,7,8,9},且若a∈M,则10-a∈M,求集合M的个数
解:∵M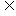 {1,2,3,4,5,6,7,8,9},且若a∈M,则10-a∈M
{1,2,3,4,5,6,7,8,9},且若a∈M,则10-a∈M
∴(1,9)、(2,8) 、(3,7) 、(4,6)、 (5)每组中的数要么同属于M,要么同不属于M,也就是这五组数可取一组、两组、三组、四组或五组。共有 25-1=31个
[例3]已知集合A={x|x2-3x+2=0},B={x|x2-mx+2=0},且A∩B=B,求实数m范围。
解:A={1,2},A∩B=B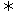 B
B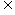 A
A
根据集合B中元素个数分类:B=φ,B={1}或{2},B={1,2}
当B=φ时,△=m2-8<0 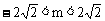
当B={1}或{2}时,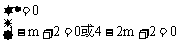 ,m无解
,m无解
当B={1,2}时,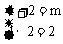 解得 m=3
解得 m=3
综上所述,m=3或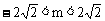
特别提醒:分类讨论是中学数学的重要思想,要做到不重不漏.本题中不要漏掉B=φ,和当B={1}或{2}时的△=0.
[例4]已知集合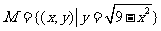

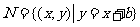 且
且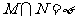 ,
,
求实数b的取值范围。
解:点集M是一个半圆,点集N是随b变
化的一组平行直线. 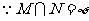 ,
,
∴两点集M与N无公共点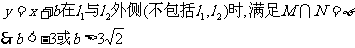
方法提炼:数形结合。
[研究.欣赏] 求1到200这200个数中既不是2的倍数,
又不是3的倍数,也不是5的倍数的自然数共有多少个?
思路.方法:“正难则反”,先求出200个数不满足条件的,即能被2或3或5整除的自然数个数,再从200中减去。
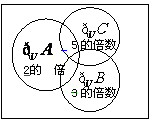 解:设不能被2、3、5整除的数的集合分别是A、B、C,则符合条件的数的集合为A∩B∩C,不符全条件的数的集合为:
解:设不能被2、3、5整除的数的集合分别是A、B、C,则符合条件的数的集合为A∩B∩C,不符全条件的数的集合为: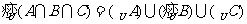 ,如图先画出文氏图,不难看出不符合的数共有:
,如图先画出文氏图,不难看出不符合的数共有:
(200÷2)+[200÷3]+(200÷5)
6.(2006全国I)设集合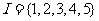 ,选择
,选择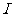 的两个非空子集
的两个非空子集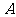 和
和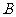 ,要使
,要使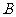 中最小的数大于
中最小的数大于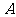 中最大的数,则不同的选择方法共有
中最大的数,则不同的选择方法共有
答案:1-4、DBAB; 5、B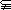 A,A∈C,B∈C; 6、49种。
A,A∈C,B∈C; 6、49种。
5.已知集合A={0,1},B={x|x∈A,x∈N*},C={x|x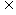 A},则A、B、C之间的关系是___________________.
A},则A、B、C之间的关系是___________________.
4.(2006湖北).有限集合S中元素的个数记作card(S)。设A、B都为有限集合,给出下列命题: ( )
①A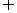 B=
B=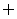 的充要条件是card(A
的充要条件是card(A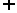 B)=cad(A)+cad(B);
B)=cad(A)+cad(B);
②A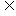 B的必要条件是cad(A)
B的必要条件是cad(A) card(B);
card(B);
③A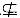 B的充分条件是cad(A)
B的充分条件是cad(A) card(B);
card(B);
④A=B的充要条件是cad(A)=card(B).
其中真命题的序号是
A.③④ B.①② C. ①④ D. ②③
3.(2006江苏)若A、B、C为三个集合,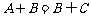 ,则一定有 ( )
,则一定有 ( )
(A)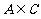 (B)
(B)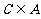 (C)
(C)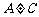 (D)
(D)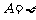
2.(2002全国)设集合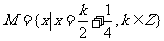 ,
,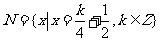 ,则( )
,则( )
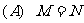 (B)M
(B)M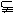 N
(C)M
N
(C)M N
N 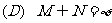
1.(2005北京西城区抽样测试)已知集合A={x∈R|x<5-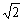 },B={1,2,3,4},则(
},B={1,2,3,4},则(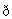 RA)∩B等于 ( )
RA)∩B等于 ( )
A.{1,2,3,4} B.{2,3,4} C.{3,4} D.{4}
6.温馨提示:注意读懂集合符号语言的意思,看清集合中元素的一般形式和元素的属性;注意区别:
∈与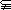 与
与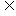 ,a与{a}、φ与{φ}与{0},{(1,2)}与{1,2},
,a与{a}、φ与{φ}与{0},{(1,2)}与{1,2},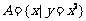 与
与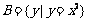 与
与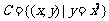 ,是各不相同的。
,是各不相同的。
4.常用运算性质及一些重要结论
①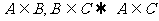 ; A
; A B,B
B,B C
C 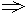 A
A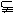 C
C
②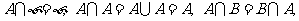
(3) 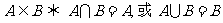
(4) 
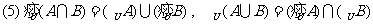
5*.并集中元素的个数:借助文氏图分析可得
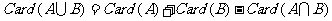
Card(A∪B∪C)=card(A)+ card(B)+ card(C)-card(A∩B) -card(A∩C) -card(C∩B)+card(A∩B∩C)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com