
6、某校高三级有三位数学老师,为方便学生,从星期一到星期五每天都安排数学教师值班,并且星期一安排两位老师值班,若每位老师每周值班两天,则一周内安排值班的方案有
种 答36
答36
4、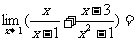 答2.
答2.
5、已知函数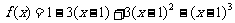 ,则
,则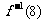 =
.答0
=
.答0
3、已知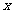 ,
,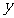 满足
满足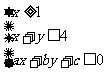 且目标函数
且目标函数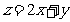 的最大值为7,最小值为1,则
的最大值为7,最小值为1,则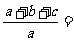 ( )
( )
A.-2 B.2 C.1 D.-1答A
2、已知: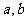 均为正数,
均为正数,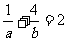 ,则使
,则使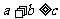 恒成立的
恒成立的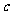 的取值范围是( )答A
的取值范围是( )答A
A. B.
B.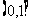 C.
C. D.
D.

1、设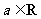 ,函数
,函数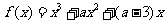 的导函数是
的导函数是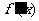 ,若
,若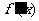 是偶函数,则曲线
是偶函数,则曲线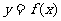 在原点处的切线方程为( )答A
在原点处的切线方程为( )答A
A. B.
B. 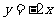 C.
C. 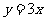 D.
D. 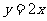
10、[解析]依题意,直线l显然不平行于坐标轴,故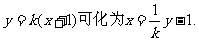
将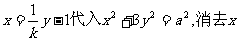 ,得
,得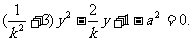 ①
①
由直线l与椭圆相交于两个不同的点,得
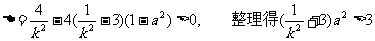 ,即
,即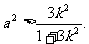
(II)解:设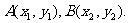 由①,得
由①,得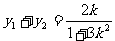
因为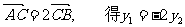 ,代入上式,得
,代入上式,得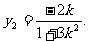
于是,△OAB的面积 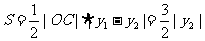
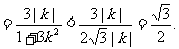
其中,上式取等号的条件是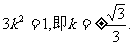 由
由
将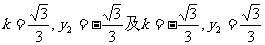 这两组值分别代入①,均可解出
这两组值分别代入①,均可解出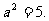
所以,△OAB的面积取得最大值的椭圆方程是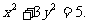
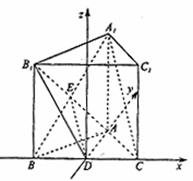
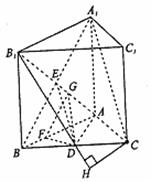
9、[解析]解法一(I)证明:连接A1B,设A1B∩AB1 = E,连接DE.
∵ABC-A1B1C1是正三棱柱,且AA1 = AB,∴四边形A1ABB1是正方形,
∴E是A1B的中点,又D是BC的中点,∴DE∥A1C.
∵DE 平面AB1D,A1C
平面AB1D,A1C 平面AB1D,∴A1C∥平面AB1D.
平面AB1D,∴A1C∥平面AB1D.
(II)解:在面ABC内作DF⊥AB于点F,在面A1ABB1内作FG⊥AB1于点G,连接DG.∵平面A1ABB1⊥平面ABC, ∴DF⊥平面A1ABB1,
∴FG是DG在平面A1ABB1上的射影, ∵FG⊥AB1, ∴DG⊥AB1
∴∠FGD是二面角B-AB1-D的平面角
设A1A
= AB = 1,在正△ABC中,DF=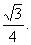
在△ABE中,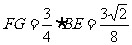 ,在Rt△DFG中,
,在Rt△DFG中,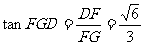 ,
,
所以,二面角B-AB1-D的大小为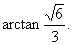
(III)解:∵平面B1BCC1⊥平面ABC,且AD⊥BC,
∴AD⊥平面B1BCC1,又AD 平面AB1D,∴平面B1BCC1⊥平面AB1D.
平面AB1D,∴平面B1BCC1⊥平面AB1D.
在平面B1BCC1内作CH⊥B1D交B1D的延长线于点H,则CH的长度就是点C到平面AB1D的距离.
由△CDH∽△B1DB,得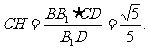 即点C到平面AB1D的距离是
即点C到平面AB1D的距离是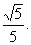
解法二:建立空间直角坐标系D-xyz,如图,(I)证明:连接A1B,设A1B∩AB1 = E,连接DE.
设A1A = AB = 1,
则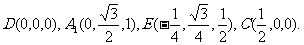
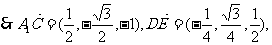
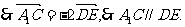
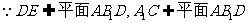 ,
,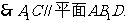
(II)解: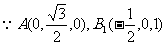 ,
, 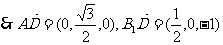 ,
,
设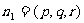 是平面AB1D的法向量,则
是平面AB1D的法向量,则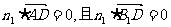 ,
,
故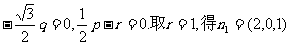 ;同理,可求得平面AB1B的法向量是
;同理,可求得平面AB1B的法向量是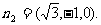
设二面角B-AB1-D的大小为θ, ,∴二面角B-AB1-D为
,∴二面角B-AB1-D为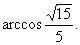
(III)解由(II)得平面AB1D的法向量为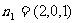 ,
,
取其单位法向量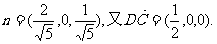 ∴点C到平面AB1D的距离
∴点C到平面AB1D的距离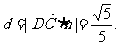
8、[解析](1)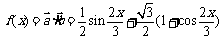
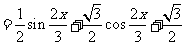
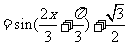 .
.
令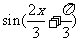 =0,得
=0,得 .而y=
.而y=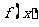 的图象可由
的图象可由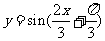 向上平移
向上平移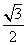 个单位得到,故所求对称中心的坐标为
个单位得到,故所求对称中心的坐标为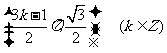 .
.
(2)由已知b2=ac,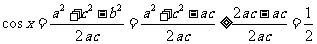
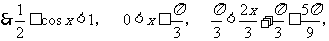
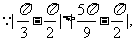
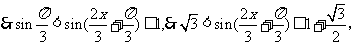
 即
即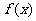 的值域为
的值域为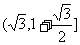 .综上所述,
.综上所述,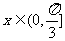 ,
,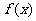 值域为
值域为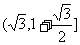 .
.
7、[解析](1):记“抛掷1枚硬币1次出现正面向上”为事件A,P(A)=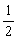
抛掷15枚均匀的硬币一次相当于做15次独立的重复试验,
根据n次独立重复试验中事件A发生k次的概率公式,记至多有1枚正面向上的概率为P1,则P1=P(0)+P(1)=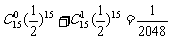
(2):记正面向上为奇数枚的概率为P2,记正面向上为偶数枚的概率为P3,则有
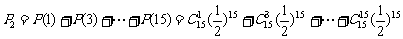
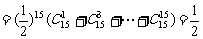
又“出现正面向上为奇数枚”的事件与“出现正面向上为偶数枚”的事件是对立事件
∴P3=1-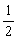 =
=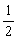 .∴出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率相等.
.∴出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率相等.
6、[解析]:本题是一道改编题,利用函数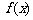 的图像信息得出
的图像信息得出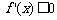 的解集是
的解集是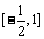 ,
,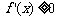 的解集是
的解集是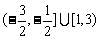 ,从而由
,从而由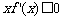 ,得
,得 ,从而
,从而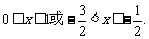
答案: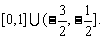
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com