
课本P36练习:1,2;P36-38习题:3.
答案:练习:1.⑴ ;⑵
;⑵ ;⑶
;⑶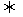 ;⑷
;⑷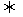 .
.
2.⑴充分而不必要的条件;⑵充分而不必要的条件;
⑶充要条件;⑷必要而不充分的条件.
例(P35例2)指出下列各组命题中,p是q的什么条件(在“充分而不必要条件”、“必要而不充分条件”、“充要条件”、“既不充分也不
必要条件”中选出一种)?
⑴p:(x-2)(x-3)=0;q:x-2=0.
⑵p:同位角相等;q:两直线平行.⑶p:x=3;q:x2=9.
⑷p:四边形的对角线相等;q:四边形是平行四边形.
解:⑴∵(x-2)(x-3)=0 x-2=0,(x-2)(x-3)=0
x-2=0,(x-2)(x-3)=0 x-2=0,
x-2=0,
∴p是q的必要而不充分的条件;
⑵∵同位角相等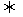 两直线平行,∴p是q的充要条件;
两直线平行,∴p是q的充要条件;
⑶∵x=3 x2=9, x=3
x2=9, x=3 x2=9,∴p是q的充分而不必要的条件;
x2=9,∴p是q的充分而不必要的条件;
⑷∵四边形的对角线相等 四边形是平行四边形,四边形的对角线相等
四边形是平行四边形,四边形的对角线相等 四边形是平行四边形,
四边形是平行四边形,
∴p是q的既不充分也不必要的条件.
⒈什么是充要条件?
如果既有p q,又有q
q,又有q p,就记作p
p,就记作p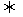 q.此时,p既是q的充分条件,p又是q的必要条件,我们就说,p是q的充分必要条件,简称充要条件.(当然此时也可以说q是p的充要条件)
q.此时,p既是q的充分条件,p又是q的必要条件,我们就说,p是q的充分必要条件,简称充要条件.(当然此时也可以说q是p的充要条件)
例如,“x=0,y=0”是“x2+y2=0”的充要条件;“三角形的三条边相等”是“三角形的三个角相等”的充要条件.
说明:⑴符号“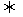 ”叫做等价符号.“p
”叫做等价符号.“p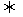 q”表示“p
q”表示“p q且p
q且p q”;也表示“p等价于q”. “p
q”;也表示“p等价于q”. “p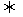 q”有时也用“p
q”有时也用“p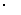 q”;
q”;
⑵“充要条件”有时还可以改用“当且仅当”来表示,其中“当”表示“充分”,“仅当”表示“必要”.
⒉几个相关的概念
若p q,但p
q,但p q,则说p是q的充分而不必要条件;
q,则说p是q的充分而不必要条件;
若p q,但p
q,但p q,则说p是q的必要而不充分条件;
q,则说p是q的必要而不充分条件;
若p q,且p
q,且p q,则说p是q的既不充分也不必要条件.
q,则说p是q的既不充分也不必要条件.
例如,“x>2”是“x>1”的充分而不必要的条件;“x>1”是“x>2”的必要而不充分的条件;“x>0 ,y>0”是“x+y<0”的既不充分也不必要的条件.
⒊充要条件的判断方法
四种“条件”的情况反映了命题的条件与结论之间的因果关系,所以在判断时应该:
⑴确定条件是什么,结论是什么;
⑵尝试从条件推出结论,从结论推出条件(方法有:直接证法或间接证法);
⑶确定条件是结论的什么条件.
4.怎样用集合的观点对“充分”、“必要”、“充要”三种条件进行概括?
答:有两种说法:⑴若A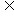 B,则A是B的充分条件,B是A的必要条件;若A=B,则A是B的充要条件(此时B也是A的充要条件).
B,则A是B的充分条件,B是A的必要条件;若A=B,则A是B的充要条件(此时B也是A的充要条件).
在含有变量的命题中,凡能使命题为真的变量x的允许值集合,叫做此命题的真值集合.
⑵若p q,说明p的真值集合
q,说明p的真值集合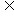 q的真值集合,则p是q的充分条件,q是p的必要条件;若p
q的真值集合,则p是q的充分条件,q是p的必要条件;若p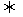 q,说明p,q的真值集合相等,即p,q等价,则p是q充要条件(此时q也是p的充要条件).
q,说明p,q的真值集合相等,即p,q等价,则p是q充要条件(此时q也是p的充要条件).
⒈什么叫做充分条件?什么叫做必要条件?
若p q(或若┐q
q(或若┐q ┐p),则说p是q的充分条件,q是p的必要条件.
┐p),则说p是q的充分条件,q是p的必要条件.
⒉指出下列命题中,p是q的什么条件,q是p的什么条件:
⑴p:x>2,q:x>1;⑵p:x>1,q:x>2;
⑶p:x>0 ,y>0,q:x+y<0;⑷p:x=0,y=0,q:x2+y2=0.
解:⑴∵x>2 x>1,∴p是q的充分条件,q是p的必要条件.
x>1,∴p是q的充分条件,q是p的必要条件.
⑵∵x>1 x>2,但x>2
x>2,但x>2 x>1,∴p是q的必要条件,q是p的充分条件.
x>1,∴p是q的必要条件,q是p的充分条件.
⑶∵x>0
,y>0 x+y<0,x+y<0
x+y<0,x+y<0 x>0
,y>0,∴p不是q的充分条件,p也不是q的必要条件;q不是p的充分条件,q也不是p的必要条件.
x>0
,y>0,∴p不是q的充分条件,p也不是q的必要条件;q不是p的充分条件,q也不是p的必要条件.
⑷∵x=0,y=0 x2+y2=0,∴p是q的充分条件,q是p的必要条件;又x2+y2=0
x2+y2=0,∴p是q的充分条件,q是p的必要条件;又x2+y2=0 x=0,y=0,∴q是p的充分条件,p是q的必要条件.
x=0,y=0,∴q是p的充分条件,p是q的必要条件.
⒊在问题⑷中,p既是q的充分条件,p又是q的必要条件,此时,我们统说,p是q的充分必要条件,简称充要条件.下面我们用数学语言来表述这个概念.
22.下面几句诗写出了山村的美丽风光,你见过这样的山村景色么?请你为这个美丽的小山标写一句广告词,要求运用某种修辞手法。
(1)绿树村边合,青山郭外斜。
(2)一水护田将绿绕,两山排闼送青来。
(3)山重水复疑无路,柳暗花明又一村。
广告词: 。
21.共青团中央、全国学联等机构共同发布的《2009年中国大学生消费与生活形态研究报告》表明,当代大学生群体呈现出以下特性。(4分)
① 。大学生作为无固定收入的群体、无论是必要的学费和生活费,还是休闲如乐消费,在很大程度上都依赖于家庭的经济支持,但他们又具有明显的独立意识与倾向,他们并不认为花父母的钱天经地义,大多数学生都在自筹收入。
② 。大学生追求个性释放,希望自己成为有独特风格的人,也喜欢风格独特的产品与品牌。但是这种独特是群体的独特,作为相互接触的群体,他们具有高度一致性;同时作为群体中的个体,他们希望并主动与群体保持一致,并以这种一致获得群体的认同。
根据以上表述,在下面的横线处概括这两个特性。(每处不超过10个字)
① ②
15.填空。(6分)
(1)德国作家 的诗剧《浮士德》,表现了启蒙思想家对真理的探索。
(2)诗人闻一多、徐志摩等以及提倡格律诗而独树一帜,形成了现代诗史上一个重要的诗歌流派,人称“ 诗派”或“格律诗派”,代表作有《死水》《再别康桥》。
(3)荀子在《劝学》中强调学习的重要性,说:“君子生非异也。 ”
①王安石在《游褒禅山记》中借浏览华山洞强调外物助人的重要,说:“有志与力,而不随以怠, ,②亦不能至也。”苏洵在《六国论》中强调人才对于国家的重要说:“以赂秦之地封天下之谋臣, ,③并力西向,则吾恐秦人食之不得下咽也。”曹操在《短歌行》中表现了对人才的渴求,“ ,④悠悠我心。”
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com