
4.人体免疫球蛋白由4条肽链构成,共有764个氨基酸,则该蛋白质分子中至少含有游离
的氨基和羧基数分别是 ( )
A.764和764 B.760和760 C.762和762 D.4和4
3.当生物新陈代谢旺盛、生长迅速时,通常结合水与自由水的比应该 ( )
A.不变 B.降低 C.升高 D.不确定
2.观察玻片标本时,若发现视野上方较暗下方较亮,应调节 ( )
A.目镜 B.物镜 C.转换器 D.反光镜
一分题(共8分)
1.下列人类的疾病中,不是由病毒引起的 ( )
A.腮腺炎 B.乙型肝炎 C.肺结构 D.脊髓灰质炎症
23.已知函数 (
( 为实常数)
为实常数)
(1)若 ,作函数
,作函数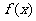 的图像;
的图像;
(2)设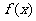 在区间
在区间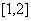 上的最小值为
上的最小值为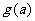 ,求
,求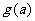 的表达式:
的表达式:
(3)设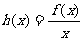 ,若函数
,若函数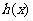 在区间
在区间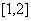 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.
22.斜率为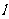 的直线过抛物线
的直线过抛物线 的焦点,且与抛物线交于两点
的焦点,且与抛物线交于两点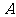 、
、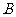 .
.
(1)求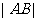 的值;
的值;
(2)将直线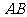 按向量
按向量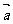 =(-2,0)平移得直线
=(-2,0)平移得直线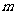 ,
,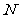 是
是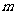 上的动点,求
上的动点,求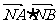 的最小值.
的最小值.
(3)设 (2,0),
(2,0),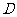 为抛物线
为抛物线 上一动点,证明:存在一条定直线
上一动点,证明:存在一条定直线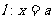 ,使得
,使得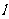 被以
被以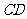 为直径的圆截得的弦长为定值,并求出直线
为直径的圆截得的弦长为定值,并求出直线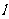 的方程.
的方程.
21.如图,在四棱锥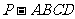 中,底面
中,底面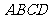 是边长为2的菱形,∠
是边长为2的菱形,∠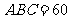 °,
°,
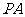 ⊥平面
⊥平面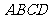 ,
,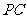 与平面
与平面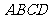 所成角的大小为
所成角的大小为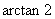 ,
, 为
为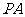 的中点.
的中点.
(1)求四棱锥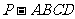 的体积;
的体积;
 (2)求异面直线
(2)求异面直线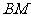 与
与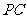 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).
20.已知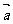 =
=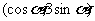 ,
,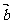 =
=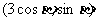 ,
,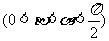 是平面上的两个向量
是平面上的两个向量
(1)试用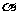 、
、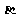 表示
表示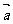 ·
·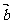 .
.
(2)若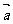 ·
·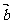 =
=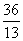 ,且
,且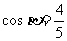 ,求
,求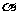 的值.(结果用反三角函数值表示)
的值.(结果用反三角函数值表示)
19.设数列{ }的前
}的前 项和为
项和为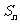 ,
,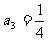 .对任意
.对任意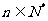 ,向量
,向量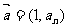 ,
,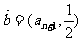 满足
满足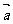 ⊥
⊥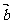 ,求
,求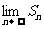 .
.
18.已知关于 的不等式
的不等式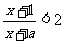 的解集为
的解集为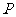 ,若
,若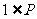 ,则实数
,则实数 的取值范围为( )
的取值范围为( )
A.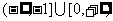 B.
B.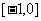
C.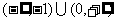 D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com