
20.设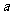 为实数,函数
为实数,函数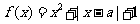 ,
,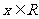 .
.
(1)讨论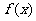 的奇偶性; (2)求
的奇偶性; (2)求 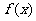 的最小值.
的最小值.
19.已知函数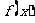 是定义在
是定义在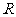 上的奇函数,当
上的奇函数,当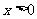 时,
时,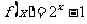 ,求⑴
,求⑴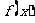 ;⑵解不等式
;⑵解不等式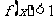 .
.
18.证明函数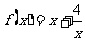 在
在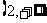 上是增函数.
上是增函数.
17.已知:集合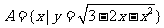 ,集合
,集合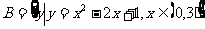 ,求
,求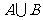 .
.
16.设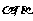 是方程
是方程
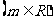 的两个实根,则
的两个实根,则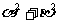 的最小值为 .
的最小值为 .
15.质量为1某物质经过10年衰减为原来的一半, 那么经过 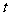 年, 此物质的质量是 .
年, 此物质的质量是 .
14.已知奇函数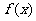 是定义在
是定义在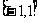 上的增函数,则不等式
上的增函数,则不等式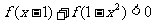 的解集为
.
的解集为
.
13.符合条件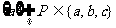 的集合
的集合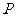 的个数是
个.
的个数是
个.
12.下列函数中值域为(0,+∞)的是 ( )
A.
y=5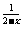 B.y=
B.y=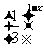 C.y=
C.y= D.y=
D.y=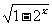
第Ⅱ卷(非选择题 共60分)
11.设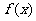 是奇函数,且在
是奇函数,且在 内是增函数,又
内是增函数,又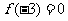 ,则
,则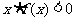 的解集是
的解集是
( )
A.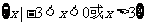 B.
B.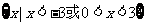
C.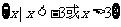 D.
D.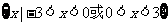
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com