
[例1](1)已知 为第四象限角,化简:
为第四象限角,化简:
(2)已知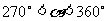 ,化简
,化简
(3) tan20°+4sin20°
解:(1)因为 为第四象限角
为第四象限角
所以原式=

(2)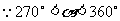 ,
,
所以原式=

(3) tan20°+4sin20°=
=

(另法:可以利用和差化积)
◆思路方法:1.化简的一般原则是:化单角或同角,函数名称少,没有根式,能求值的要求出值;
2.根式形式的三角函数式化简常采用有理化如(1)或升幂公式如(2)
[例2](1)已知sin(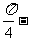 x)=
x)= ,0<x<
,0<x< ,求
,求 的值。
的值。
(2)已知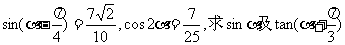 .
.
解:(1)解法1:∵ ,∴cos(
,∴cos( +x)=sin(
+x)=sin( -x)
-x)
又cos2x=sin(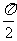 -2x)=sin2(
-2x)=sin2( -x)=2sin(
-x)=2sin( -x)cos(
-x)cos( -x)
-x)
∴ =2 cos(
=2 cos( -x)=2
-x)=2
解法2:

∴

 =
=
(2)解法一:由题设条件,应用两角差的正弦公式得

即 ①
①
由题设条件,应用二倍角余弦公式得
 故
故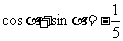 ②
②
由①式和②式得
 .因此,
.因此,
由两角和的正切公式

解法二:由题设条件,应用二倍角余弦公式得

解得
由
由于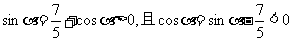 ,
,
故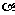 在第二象限,于是
在第二象限,于是 .
.
从而
以下同解法一.
◆提炼方法:(1)题:变换角: 及
及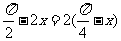 ,利用余角间的三角函数的关系便可求之。
,利用余角间的三角函数的关系便可求之。
(2)题是利用sinα±cosα与sinα、cosα的关系,求出了sinα、cosα;提醒我们解题思路的灵活性。
[例3]若 ,
,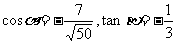 ,求α+2β。
,求α+2β。
解:∵ ,
,
∴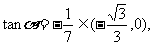

∴ ,α+2β
,α+2β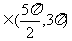 ,
,
又tan2β= ,
, ,
,
∴α+2β=
◆思路方法:“给值求角分两步”:第一步,求出此角的某一三角函数值;第二步,根据此角的范围求出此角。在确定角的范围时,要尽可能地将角的范围缩小,否则易增解。
[例4]求证:
证:左边=

右边=
所以左边=右边,即等式成立。
◆思路点拨:切化弦,降次.或左右归一.
[研讨.欣赏]在ΔABC中,设tanA+tanC=2tanB,求证cos(B+C-A)=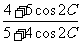 .
.
证明:
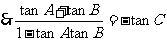

由条件得


 而
而 ,
,
又
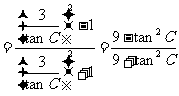
而

 cos(B+C-A)=
cos(B+C-A)=
法2:由tanA+tanC=-2tan(A+c)得tanAtanC=3…
6.切化弦,原式=
法2: =tan60°,原式=
=tan60°,原式=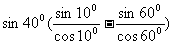
=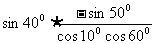 =
=
2.由已知: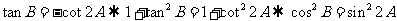 ,又是锐角三角形,选A;
4.用韦达定理,
,又是锐角三角形,选A;
4.用韦达定理, ,求tan(α+β); 5.
,求tan(α+β); 5. 
6. 计算 =________。
=________。
◆简答:1-4.AABA;
5. 已知α+β= ,且
,且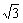 (tanαtanβ+c)+tanα=0(c为常数),那么tanβ=______
(tanαtanβ+c)+tanα=0(c为常数),那么tanβ=______
4. 已知tanα,tanβ是方程 两根,且α,β
两根,且α,β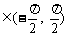 ,则α+β=( )
,则α+β=( )
A、 B、
B、 或
或 C、
C、 或
或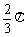 D、
D、 。
。
3.已知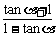 =2007,则
=2007,则 的值为
( )
的值为
( )
A、2006 B、2007 C、2009 D、2010
2.锐角三角形的内角 、
、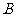 满足
满足 ,则有
( )
,则有
( )
A. B.
B.
C. D.
D.
1.(2006湖北)若ΔABC的内角A满足sin2A=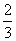 ,则sinA+cosA= ( )
,则sinA+cosA= ( )
A.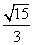 B. -
B. -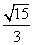 C.
C.  D.-
D.-
4.无论是化简还是证明都要注意:
(1)角度的差异与联系;
(2)函数名称间的变换和联系,升降幂,化切为弦是常用手段;
(3)角的范围对三角函数取值、符号的影响;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com