
1.7.1、 静止流体中的压强
(1)静止流体内部压强的特点
在静止流体内任何一点处都有压强,这一压强与方向无关仅与该点的深度有关;相连通的静止流体内部同一深度上各点的压强相等。
关于流体内部的压强与方向无关,可以证明如下:
 在静止流体中的某点处任取一个长为
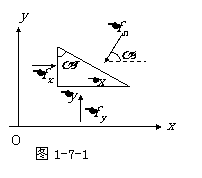
在静止流体中的某点处任取一个长为 的极小的直角三棱液柱,令其两侧面分别在竖直面内和水平面内,作其截面如图1-7-1所示,图中坐标轴x沿水平方向,坐标轴y沿竖直方向,以
的极小的直角三棱液柱,令其两侧面分别在竖直面内和水平面内,作其截面如图1-7-1所示,图中坐标轴x沿水平方向,坐标轴y沿竖直方向,以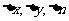 分别表示此液柱截面三角形的三条边长,且以
分别表示此液柱截面三角形的三条边长,且以 表示此截面三角形的一个锐角如图1-7-1,又以
表示此截面三角形的一个锐角如图1-7-1,又以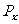 ,
,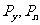 分别表示对应侧面上压强的大小,则各侧面所受压力的大小分别为:
分别表示对应侧面上压强的大小,则各侧面所受压力的大小分别为:
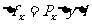
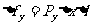
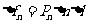
由此液柱很小,则其重力将远小于它的一个侧面所受到的压力,故可忽略其重力的作用。则由此液柱的平衡条件知上述三力应互相平衡,乃有:
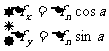
即 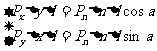
注意到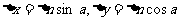 ,代入上式便得
,代入上式便得
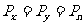
说明在流体内部的同一点处向各个方向的压强是相等的。
(2)静止流体内部压强的大小
若静止流体表面处的压强为P。(通常即为与该流体表面相接触的气体的压强),流体的密度为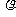 ,则此流体表面下深度为h处的压强为
,则此流体表面下深度为h处的压强为
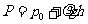
由上式可见,在静止流体内部高度差为 的两点间的压强差为
的两点间的压强差为
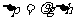
1.6.3、稳度
物体稳定的程度叫稳度,一般说来,使一个物体的平衡遭到破坏所需的能量越多,这个平衡的稳度就越高。稳度与重心的高度及支面的大小有关,重心越低,支面越大,稳度越大。
§1.7 流体静力学
流体并没有一定的开头可以自由流动,但具有一定的密度,一般认为理想流体具有不可压缩的特征。
1.6.2、物体平衡的种类
物体的平衡分为三类:
稳定平衡 处于平衡状态的物体,当受到外界的扰动而偏离平衡位置时,如果外力或外力矩促使物体回到原平衡位置,这样的平衡叫稳定平衡,处于稳定平衡的物体,偏离平衡位置时,重心一般是升高的。
不稳定平衡 处于平衡状态的物体,当受到外界的扰动而偏离平衡位置时,如果外力或外力矩促使物体偏离原来的平衡位置,这样的平衡叫不稳定平衡,处于不稳定平衡的物体,偏离平衡位置时,重心一般是降低的。
随遇平衡 处于平衡状态的物体,当受到外界扰动而偏离平衡位置时,物体受到的合外力或合力矩没有变化,这样的平衡叫随遇平衡,处于随遇平衡的物体,偏离平衡位置后,重心高度不变。
在平动方面,物体不同方面上可以处于不同的平衡状态,在转动方面,对不同方向的转轴可以处于不同的平衡状态。例如,一个位于光滑水平面上的直管底部的质点,受到平行于管轴方向的扰动时,处于随遇平衡状态;受到与轴垂直方向的扰动时,处于稳定平衡状态,一细棒,当它直立于水平桌面时,是不稳定平衡,当它平放在水平桌面时,是随遇平衡。
1.6.1、重心
物体的重心即重力的作用点。在重力加速度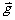 为常矢量的区域,物体的重心是惟一的(我们讨论的都是这种情形),重心也就是物体各部分所受重力的合力的作用点,由于重力与质量成正比,重力合力的作用点即为质心,即重心与质心重合。
为常矢量的区域,物体的重心是惟一的(我们讨论的都是这种情形),重心也就是物体各部分所受重力的合力的作用点,由于重力与质量成正比,重力合力的作用点即为质心,即重心与质心重合。
求重心,也就是求一组平行力的合力作用点。相距L,质量分别为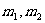 的两个质点构成的质点组,其重心在两质点的连线上,且
的两个质点构成的质点组,其重心在两质点的连线上,且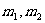 与相距分别为:
与相距分别为:
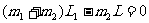
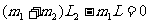
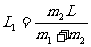
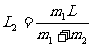
均匀规则形状的物体,其重心在它的几何中心,求一般物体的重心,常用的方法是将物体分割成若干个重心容易确定的部分后,再用求同向平行力合力的方法找出其重心。
物体重心(或质心)位置的求法
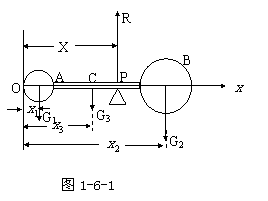
我们可以利用力矩和为零的平衡条件来求物体的重心位置。如图1-6-1由重量分别为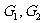 的两均匀圆球和重量为
的两均匀圆球和重量为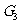 的均匀杆连成的系统,设立如图坐标系,原点取在A球最左侧点,两球与杆的重心的坐标分别为
的均匀杆连成的系统,设立如图坐标系,原点取在A球最左侧点,两球与杆的重心的坐标分别为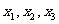 ,系统重心在P点,我们现在求其坐标x。设想在P处给一支持力R,令
,系统重心在P点,我们现在求其坐标x。设想在P处给一支持力R,令 达到平衡时有:
达到平衡时有:
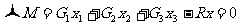
∴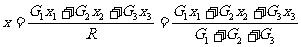
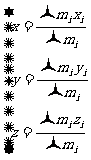
这样就得出了如图所示的系统的重心坐标。若有多个物体组成的系统,我们不难证明其重心位置为:
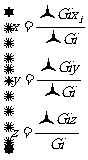
一般来说,物体的质心位置与重心位置重合,由上面公式很易得到质心位置公式:
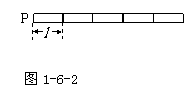
如图1-6-2,有5个外形完全一样的均匀金属棒首尾相接焊在一起,从左至右其密度分别为ρ、⒈1ρ、⒈2ρ、⒈3ρ、⒈4ρ,设每根棒长均为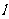 ,求其质心位置,若为n段,密度仍如上递增,质心位置又在什么地方?
,求其质心位置,若为n段,密度仍如上递增,质心位置又在什么地方?
解:设整个棒重心离最左端距离为x,则由求质心公式有
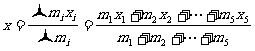

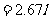
若为n段,按上式递推得:

将坐标原点移到第一段棒的重心上,则上式化为:
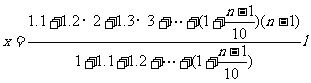
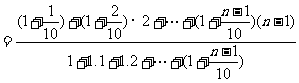
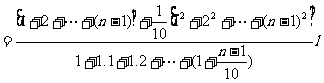
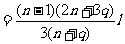
 例、如图1-6-3所示,A、B原为两个相同的均质实心球,半径为R,重量为G,A、B球分别挖去半径为
例、如图1-6-3所示,A、B原为两个相同的均质实心球,半径为R,重量为G,A、B球分别挖去半径为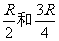 的小球,均质杆重量为
的小球,均质杆重量为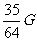 ,长度
,长度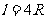 ,试求系统的重心位置。
,试求系统的重心位置。
解:将挖去部份的重力,用等值、反向的力取代,图示系统可简化为图1-1-31所示平行力系;其中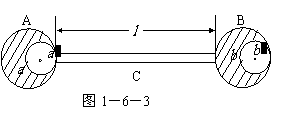
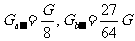 。设重心位置为O,则合力
。设重心位置为O,则合力
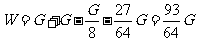
且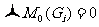 即
即
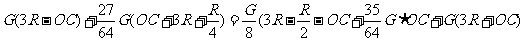
 OC=0.53R
OC=0.53R
1.4.3、有固定转动轴物体的平衡
有固定转轴的物体,若处于平衡状态,作用于物体上各力的力矩的代数和为零。
§1.5 一般物体的平衡
力对物体的作用可以改变物体的运动状态,物体各部位所受力的合力对物体的平动有影响,合力矩对物体的转动有影响。如果两种影响都没有,就称物体处于平衡状态。因此,一般物体处于平衡时,要求物体所受合外力为零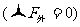 和合力矩为零
和合力矩为零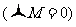 同时满足,一般物体的平衡条件写成分量式为
同时满足,一般物体的平衡条件写成分量式为
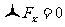
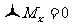
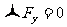
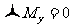
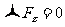
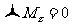
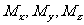 分别为对x轴、y轴、z轴的力矩。
分别为对x轴、y轴、z轴的力矩。
由空间一般力系的平衡方程,去掉由力系的几何性质能自动满足的平衡方程,容易导出各种特殊力系的独立平衡方程。
如平面力系(设在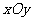 平面内),则
平面内),则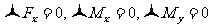 自动满足,则独立的平衡方程为:
自动满足,则独立的平衡方程为:
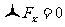
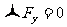
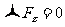
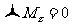 这一方程中的转轴可根据需要任意选取,一般原则是使尽量多的力的力臂为零。
这一方程中的转轴可根据需要任意选取,一般原则是使尽量多的力的力臂为零。
平面汇交力系与平面平行力系的独立方程均为二个,空间汇交力系和空间平行力系的独立平衡方程均为三个。
§1.6 平衡的稳定性
1.4.2、力偶和力偶矩
 一对大小相等、方向相反但不共线的力称为力偶。如图1-4-2中
一对大小相等、方向相反但不共线的力称为力偶。如图1-4-2中 即为力偶,力偶不能合成为一个力,是一个基本力学量。对于与力偶所在平面垂直的任一轴,这一对力的力矩的代数和称为力偶矩,注意到
即为力偶,力偶不能合成为一个力,是一个基本力学量。对于与力偶所在平面垂直的任一轴,这一对力的力矩的代数和称为力偶矩,注意到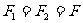 ,不难得到,M=Fd,式中d为两力间的距离。力偶矩与所相对的轴无关。
,不难得到,M=Fd,式中d为两力间的距离。力偶矩与所相对的轴无关。
1.4.1、力矩
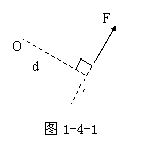 力的三要素是大小、方向和作用点。由作用点和力的方向所确定的射线称为力的作用线。力作用于物体,常能使物体发生转动,这时外力的作用效果不仅取决于外力的大小和方向,而且取决于外力作用线与轴的距离--力臂(d)。
力的三要素是大小、方向和作用点。由作用点和力的方向所确定的射线称为力的作用线。力作用于物体,常能使物体发生转动,这时外力的作用效果不仅取决于外力的大小和方向,而且取决于外力作用线与轴的距离--力臂(d)。
力与力臂的乘积称为力矩,记为M,则M=Fd,如图1-4-1,O为垂直于纸面的固定轴,力F在纸面内。
力矩是改变物体转动状态的原因。力的作用线与轴平行时,此力对物体绕该轴转动没有作用。若力F不在与轴垂直的平面内,可先将力分解为垂直于轴的分量F⊥和平行于轴的分量F∥,F∥对转动不起作用,这时力F的力矩为M=F⊥d。
通常规定 绕逆时方向转动的力矩为正。当物体受到多个力作用时,物体所受的总力矩等于各个力产生力矩的代数和。
1.3.2、推论
物体在n(n≥3)个外力作用下处于平衡状态,若其中有n-1个力为共点力,即它们的作用线交于O点,则最后一个外力的作用线也必过O点,整个外力组必为共点力。这是因为n-1个外力构成的力组为共点(O点)力,这n-1个的合力必过O点,最后一个外力与这n-1个外力的合力平衡,其作用线必过O点。
特例,物体在作用线共面的三个非平行力作用下处于平衡状态时,这三个力的作用线必相交于一点且一定共面。
§1.4 固定转动轴物体的平衡
1.3.1、共点力作用下物体的平衡条件
几个力如果都作用在物体的同一点,或者它们的作用线相交于同一点,这几个力叫作共点力。当物体可视为质点时,作用在其上的力都可视为共点力。当物体不能视为质点时,作用于其上的力是否可视为共点力要看具体情况而定。
物体的平衡包括静平衡与动平衡,具体是指物体处于静止、匀速直线运动和匀速转动这三种平衡状态。
 共点力作用下物体的平衡条件是;物体所受到的力的合力为零。
共点力作用下物体的平衡条件是;物体所受到的力的合力为零。
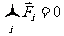
或其分量式:
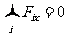
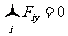
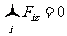
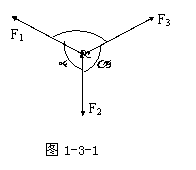
如果在三个或三个以上的共点力作用下物体处于平衡,用力的图示表示,则这些力必组成首尾相接的闭合力矢三角形或多边形;力系中的任一个力必与其余所有力的合力平衡;如果物体只在两个力作用下平衡,则此二力必大小相等、方向相反、且在同一条直线上,我们常称为一对平衡力;如果物体在三个力作用下平衡,则此三力一定共点、一定在同一个平面内,如图1-3-1所示,且满足下式(拉密定理):
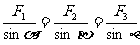
1.2.4、空间中力的投影与分解
力在某轴上的投影定义为力的大小乘以力与该轴正向间夹角的余弦,如图1-2-5中的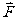 力在ox、oy、oz轴上的投影X、Y、Z分别定义为
力在ox、oy、oz轴上的投影X、Y、Z分别定义为
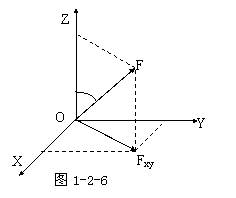
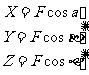
这就是直接投影法所得结果,也可如图1-2-6所示采用二次投影法。这时
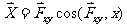
式中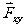 为
为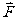 在oxy平面上的投影矢量,而
在oxy平面上的投影矢量,而
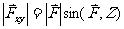
力沿直角坐标轴的分解式
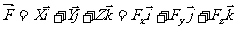
§1.3共点力作用下物体的平衡
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com