
4. 方程(x-5)( x-6)=x-5的解是( )
A.x=5 B.x=5或x=6 C.x=7 D.x=5或x=7
答案:D
3. 六月P市连降大雨,某部队前往救援,乘车行进一段路程之后,由于道路受阻,汽车无法通行,部队短暂休整后决定步行前往,则能反映部队离开驻地的距离S(千米)与时间t(小时)之间的函数关系的大致图象是( )
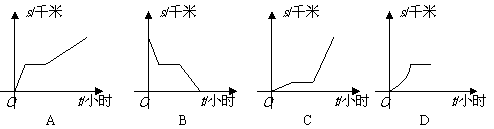
答案:A
2. 下列图形中不是轴对称图形的是( )
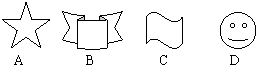
答案:C
1. 下列各式:①(-)-2=9;②(-2)0=1;③(a+b)2=a2+b2;④(-3ab3)2=9a2b6;⑤3x2-4x=-x,其中计算正确的是( )
A.①②③ B.①②④ C.③④⑤ D.②④⑤
答案:B
1.(2010年广东理19)(本小题满分12分)
某营养师要为某个儿童预定午餐和晚餐。已知一个单位的午餐含12个单位的碳水化合物6个单位蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养 中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素C.
中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预定多少个单位的午餐和晚餐?
解:设该儿童分别预订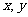 个单位的午餐和晚餐,共花费
个单位的午餐和晚餐,共花费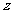 元,则
元,则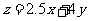 。
。
可行域为
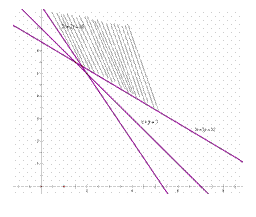
 即
即
作出可行域如图所示:
经试验发现,当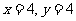 时,花费最少,为
时,花费最少,为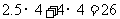 元.
元.
5.(2007年山东理14)设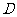 是不等式组
是不等式组 表示的平面区域,则
表示的平面区域,则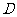 中的点
中的点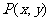 到直线
到直线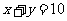 距离的最大值是_______.
距离的最大值是_______.
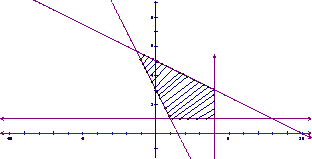
[答案]: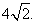 [分析]:画图确定可行域,从而确定
[分析]:画图确定可行域,从而确定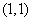 到直线直线
到直线直线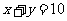 距离的最大为
距离的最大为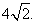
4.(2009年浙江理13)若实数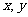 满足不等式组
满足不等式组 则
则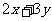 的最小值是
.
的最小值是
.
[解析]通过画出其线性规划,可知直线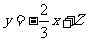 过点
过点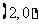 时,
时,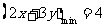
3.(2010年辽宁理14)已知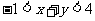 且
且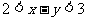 ,则
,则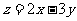 的取值范围是_______(答案用区间表示)
的取值范围是_______(答案用区间表示)
[答案](3,8)
[命题立意]本题考查了线性规划的最值问题,考查了同学们数形结合解决问题的能力。
[解析]画出不等式组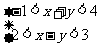 表示的可行域,在可行域内平移直线z=2x-3y,当直线经过x-y=2与x+y=4的交点A(3,1)时,目标函数有最小值z=2×3-3×1=3;当直线经过x+y=-1与x-y=3的焦点A(1,-2)时,目标函数有最大值z=2×1+3×2=8.
表示的可行域,在可行域内平移直线z=2x-3y,当直线经过x-y=2与x+y=4的交点A(3,1)时,目标函数有最小值z=2×3-3×1=3;当直线经过x+y=-1与x-y=3的焦点A(1,-2)时,目标函数有最大值z=2×1+3×2=8.
2.(2010年安徽理13)设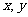 满足约束条件
满足约束条件 ,若目标函数
,若目标函数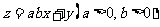 的最大值为8,则
的最大值为8,则 的最小值为________。
的最小值为________。
[答案]4[解析]不等式表示的区域是一个四边形,4个顶点是
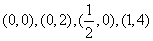 ,易见目标函数在
,易见目标函数在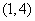 取最大值8,
取最大值8,
所以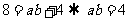 ,所以
,所以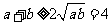 ,在
,在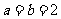 时是等号成立。所以
时是等号成立。所以 的最小值为4.
的最小值为4.
[规律总结]线性规划问题首先作出可行域,若为封闭区域(即几条直线围成的区域)则区域端点的值是目标函数取得最大或最小值,求出直线交点坐标代入得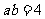 ,要想求
,要想求 的最小值,显然要利用基本不等式.
的最小值,显然要利用基本不等式.
1.( 2010年陕西理14)铁矿石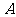 和
和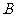 的含铁率
的含铁率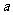 ,冶炼每万吨铁矿石的
,冶炼每万吨铁矿石的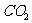 的排放量
的排放量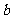 及每万吨铁矿石的价格
及每万吨铁矿石的价格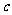 如下表:
如下表:
|
|
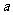 |
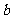 (万吨) (万吨) |
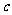 (百万元) (百万元) |
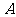 |
50% |
1 |
3 |
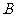 |
70% |
0.5 |
6 |
某冶炼厂至少要生产1.9(万吨)铁,若要求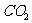 的排放量不超过
的排放量不超过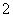 (万吨),则购买铁矿石的最少费用为
(万吨),则购买铁矿石的最少费用为 (百万元).
(百万元).
[答案]15[解析]设铁矿石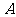 购买了
购买了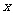 万吨,铁矿石
万吨,铁矿石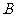 购买了
购买了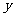 万吨,购买铁矿石的费用为
万吨,购买铁矿石的费用为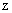 百万元,则由题设知,本题即求实数
百万元,则由题设知,本题即求实数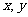 满足约束条件
满足约束条件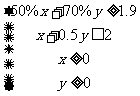 ,即
,即 (*)时,
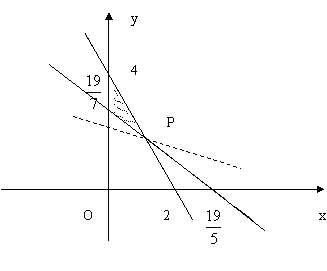
(*)时,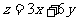 的最小值.作不等式组(*)对应的平面区域,如图阴影部分所示.现让直线
的最小值.作不等式组(*)对应的平面区域,如图阴影部分所示.现让直线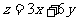 ,即
,即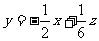 平移分析即知,当直线经过点
平移分析即知,当直线经过点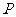 时,
时,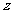 取得最小值.又解方程组
取得最小值.又解方程组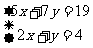 得点
得点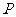 坐标为
坐标为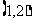 .故
.故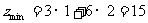 .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com