4．借助例1尝试用基本不等式解决简单的最值问题，通过例2及其变式引导学生领会运用基本不等式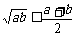的三个限制条件(一正二定三相等)在解决最值中的作用，提升解决问题的能力，体会方法与策略．

以上教学目标结合了教学实际，将知识与能力、过程与方法、情感态度价值观的三维目标融入各个教学环节．

3．结合课本的探究图形，引导学生进一步探究基本不等式的几何解释，强化数形结合的思想；

2．进一步提炼、完善基本不等式，并从代数角度给出不等式的证明，组织学生分析证明方法，加深对基本不等式的认识，提高逻辑推理论证能力；

1．通过两个探究实例，引导学生从几何图形中获得两个基本不等式，了解基本不等式的几何背景，体会数形结合的思想；

本节课我将遵循“教师的主导作用和学生的主体地位相统一的教学原则”，采用以问题为载体，以学生中心，以方法构建和能力培养为目标的教学思路，充分利用多媒体辅助教学.通过教师在教学过程中的点拨、启发，帮助学生体验和领悟函数建模的思想方法.

高一学生从初中跨越到高中，思维活跃，求知欲强，但尚未具有良好的思维水平和学习习惯.本节课从学生原有的知识基础和实际能力出发，引导学生通过主动观察、思考、动手操作、自主探究、合作学习等教学活动来寻求解决问题的方法.

通过本节课的学习，期望学生领会根据图表信息建立函数模型解决实际问题的基本思想，会利用函数建模解决一些简单的实际应用问题，培养数学应用意识和实践能力.在本节课的教学过程中，师生营造一个生动、和谐的教学氛围，让学生感受学习数学的乐趣，优化思维品质.

3.函数概念源于生产、生活实际，通过函数建模又能够解决实际问题，学生可从中领悟到“认识来源于实践又服务于实践”的辩证观点.

2.数学建模是培养学生的应用意识、创新意识、探索精神和实践能力的重要途径，通过函数建模解决实际问题可以优化学生的理性思维和求真务实的科学态度；

1.通过函数建模解决实际问题，是数学“问题解决”的教学情境之一，借此可激发学生学习数学的兴趣，增强学生学好数学的自信心；

2.在实例的分析和解决过程中，需要运用函数与方程、数形结合、分类讨论、化归转换等数学思想方法，学生可从中领悟这些数学思想方法的内涵特征.

情感、态度与价值观目标：