3、教材第79页，B组第一题(选择此题，可以进一步理解位移概念，又能为后一步的学习做好铺垫)

2、　　　　　　 教材例题

如图 2 - 7，D，E，F 依次等边三角形 ABC 的边AB，BC，AC 的中点．在以 A，B，C，D，E，F 为起点或终点的向量中，

(1)　　 找出与向量 DE 相等的向量；

(2)　　 找出与向量 DF 共线的向量．

1、　　　　　　 概念辨析

1)　　 两个长度相等的向量一定相等．

2)　　 相等向量的起点必定相同．

3)　　 平行向量就是共线向量．

4)　　 若 AB 与 CD 共线，则 A、B、C、D 四点必在同一条直线上．

5)　　 向量 a 与 b 平行，则向量 a 与 b 的方向相同或相反．

4.3 课堂练习：

3、既关注方向有又关注长度有相等向量：记作：a = b

规定： 0 与任一向量都平行或(共线)。

教师通过动画演示深化上述两个概念

问题4 由相等向量的概念知道，向量完全有它的方向和大小确定。由此，你能说说数学中的向量与物理中的矢量的异同吗？另外，向量的平行、共线与线段的平行、共线有什么区别与联系？

意图：让学生注意把向量概念与物理背景、几何背景明确区分，真正抓住向量的本质特征，完成“数学化”的过程。

2、从“长度”角度看，有模相等的向量，︱a︱ =︱ b︱

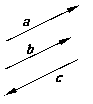
1、从“方向”角度看，有方向相同或相反的非零向量就是平行向量。

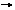　 记作：a ∥b ∥ c

任一组平行向量都可移到同一条直线上 ，所以平行向量也叫共线向量。

4.2 相等向量、平行(共线)向量概念的形成

设计活动：传花游戏

意图：通过游戏调动学生的兴趣和积极性，让学生通过亲身经历去体会相等向量与平行向量的本质特征。

归纳：

4.1.3 单位向量、零向量的概念：

问题3用有向线段表示向量，学生演板，提出问题，大家画得线段长度长短不一怎么回事？如何解决这问题？由单位长度引入单位向量

意图：这样过渡学生不会感觉新的概念是从天而降，而是进一步学习的需要

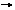
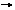归纳小结：单位向量--长度等于1个单位长度并与a同向的向量叫做a方向上的单位向量．

让演板学生回到座位之后利用这个情境提出问题，他位移的大小是什么？

归纳小结：零向量--长度(模)为0的向量，记作0，它的方向是任意的。

提问：你们认为零向量和单位向量特殊吗？它们的特殊性体现在哪？类比实数集合中的0和1.

4.1.2 向量的表示方法

问题2　 数学中，定义概念后，通常要用符号表示它。怎样把你举例中的向量表示出来呢

意图：让学生先练习力的表示，让错误呈现，激发认知冲突，最后自觉接受用带有箭头的线段(有向线段)来表示向量。(教师引导学生进一步完善)

几何表示法：　　 记作A B 　　　|A B|为AB的长度(又称模)。

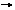
字母表示法：a、b、c……或a、b、c ……