
24、(本小题满分12分) 已知椭圆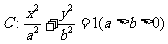 过点
过点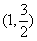 ,且离心率e=.
,且离心率e=.
(Ⅰ)求椭圆方程;
(Ⅱ)若直线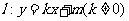 与椭圆交于不同的两点
与椭圆交于不同的两点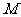 、
、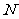 ,且线段
,且线段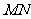 的垂直平分线过定点
的垂直平分线过定点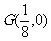 ,求
,求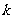 的取值范围。
的取值范围。
由题意椭圆的离心率
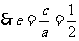
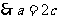
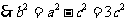
∴椭圆方程为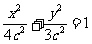 ……2分
……2分
又点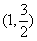 在椭圆上
在椭圆上 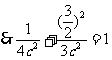
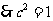
∴椭圆的方程为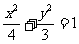 ……4分
……4分
(Ⅱ)设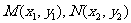 由
由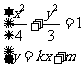
消去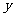 并整理得
并整理得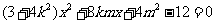 ……6分
……6分
∵直线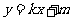 与椭圆有两个交点
与椭圆有两个交点
 ,即
,即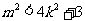 ……8分
……8分
又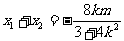
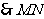 中点
中点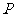 的坐标为
的坐标为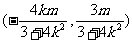 ……9分
……9分
设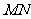 的垂直平分线
的垂直平分线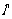 方程:
方程: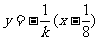
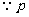 在
在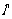 上
上 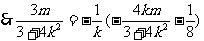 即
即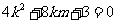
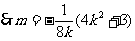 ……11分
……11分
将上式代入得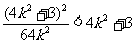
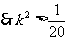
即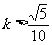 或
或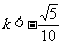
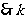 的取值范围为
的取值范围为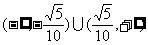
23、(东北师大附中高2008届第四次摸底考试)已知双曲线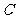 的中心在原点,对称轴为坐标轴,其一条渐近线方程是
的中心在原点,对称轴为坐标轴,其一条渐近线方程是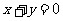 ,且双曲线
,且双曲线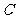 过点
过点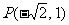 .
.
(1)求此双曲线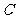 的方程;
的方程;
(2)设直线 过点
过点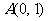 ,其方向向量为
,其方向向量为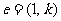
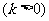 ,令向量
,令向量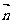 满足
满足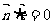 .双曲线
.双曲线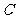 的右支上是否存在唯一一点
的右支上是否存在唯一一点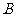 ,使得
,使得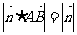 . 若存在,求出对应的
. 若存在,求出对应的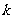 值和
值和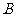 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
解:(1)设双曲线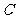 的方程为
的方程为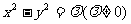 ,将点
,将点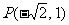 代入可得
代入可得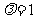 ,
,
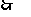 双曲线
双曲线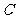 的方程为
的方程为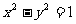 .
.
(2)依题意,直线  的方程为
的方程为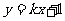
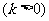 .设
.设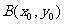 是双曲线右支上满足
是双曲线右支上满足
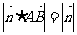 的点,结合
的点,结合
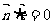 ,得
,得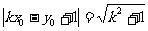 ,
,
即点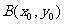 到直线
到直线 的距离
的距离 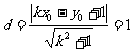
①若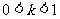 ,则直线
,则直线 与双曲线
与双曲线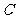 的右支相交,此时双曲线
的右支相交,此时双曲线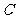 的右支上有两个点到直线
的右支上有两个点到直线 的距离为1,与题意矛盾;
的距离为1,与题意矛盾;
②若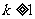 ,则直线
,则直线 在双曲线
在双曲线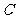 右支的上方,故
右支的上方,故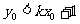 ,从而
,从而
 . 又因为
. 又因为 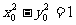 ,所以
,所以
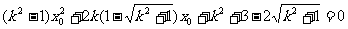 .
.
当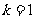 时,方程有唯一解
时,方程有唯一解
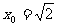 ,则
,则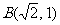 ;
;
当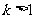 时,由
时,由 得
得
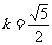 ,此时方程有唯一解
,此时方程有唯一解
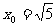 ,则
,则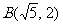
综上所述,符合条件的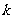 值有两个:
值有两个: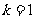 ,此时
,此时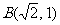 ;
;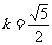 ,此时
,此时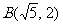 .
.
22、(东北三校2008年高三第一次联考)设椭圆C: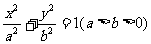 的左焦点为F,上顶点为A,过点A作垂直于AF的直线交椭圆C于另外一点P,交x轴正半轴于点Q, 且
的左焦点为F,上顶点为A,过点A作垂直于AF的直线交椭圆C于另外一点P,交x轴正半轴于点Q, 且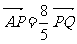
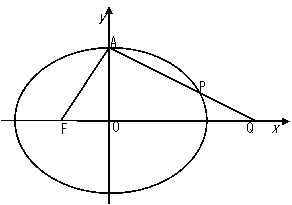 (1)求椭圆C的离心率;
(1)求椭圆C的离心率;
(2)若过A、Q、F三点的圆恰好与直线l:
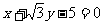 相切,求椭圆C的方程.
相切,求椭圆C的方程.
解:⑴设Q(x0,0),由F(-c,0)
A(0,b)知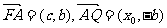
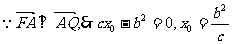 …2分
…2分
设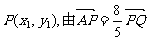 ,得
,得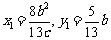 ………4分
………4分
因为点P在椭圆上,所以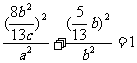 ………6分
………6分
整理得2b2=3ac,即2(a2-c2)=3ac,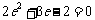 ,故椭圆的离心率e=………8分
,故椭圆的离心率e=………8分
⑵由⑴知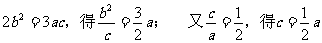 ,
,
于是F(-a,0), Q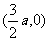
△AQF的外接圆圆心为(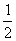 a,0),半径r=|FQ|=a…………10分
a,0),半径r=|FQ|=a…………10分
所以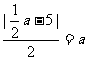 ,解得a=2,∴c=1,b=
,解得a=2,∴c=1,b=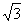 ,
,
所求椭圆方程为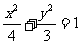
21、(东北区三省四市2008年第一次联合考试)已知中心在原点,左、右顶点A1、A2在x轴上,离心率为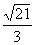 的双曲线C经过点P(6,6),动直线l经过△A1PA2的重心G与双曲线C交于不同两点M、N,Q为线段MN的中点。
的双曲线C经过点P(6,6),动直线l经过△A1PA2的重心G与双曲线C交于不同两点M、N,Q为线段MN的中点。
(1)求双曲线C的标准方程
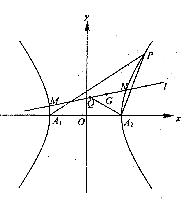 (2)当直线l的斜率为何值时,
(2)当直线l的斜率为何值时,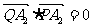 。
。
本小题考查双曲线标准议程中各量之间关系,以及直线与双曲线的位置关系。
解(1)设双曲线C的方程为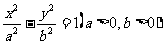
|
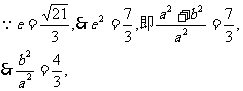
|
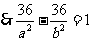
由①、②解得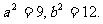
所以双曲线C的方程为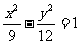 。
。
(2)由双曲线C的方程可得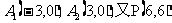
所以△A1PA2的重点G(2,2)
设直线l的方程为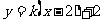 代入C的方程,整理得
代入C的方程,整理得
|
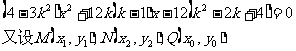

整理得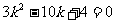
|
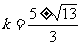
由③,可得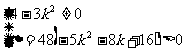
|
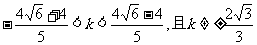
由④、⑤,得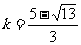
20、(四川省成都市2008届高中毕业班摸底测试)设双曲线C: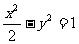 的左、右顶点分别为A1、A2,垂直于x轴的直线m与双曲线C交于不同的两点P、Q。
的左、右顶点分别为A1、A2,垂直于x轴的直线m与双曲线C交于不同的两点P、Q。
(Ⅰ)若直线m与x轴正半轴的交点为T,且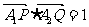 ,求点T的坐标;
,求点T的坐标;
(Ⅱ)求直线A1P与直线A2Q的交点M的轨迹E的方程;
(Ⅲ)过点F(1,0)作直线l与(Ⅱ)中的轨迹E交于不同的两点A、B,设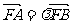 ,若
,若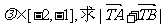 (T为(Ⅰ)中的点)的取值范围。
(T为(Ⅰ)中的点)的取值范围。
解:(Ⅰ)由题,得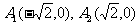 ,设
,设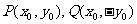
则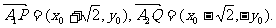
由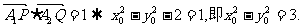 …………①
…………①
又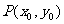 在双曲线上,则
在双曲线上,则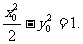 …………②
…………②
联立①、②,解得
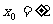
由题意, 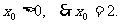
∴点T的坐标为(2,0) …………3分
(Ⅱ)设直线A1P与直线A2Q的交点M的坐标为(x,y)
由A1、P、M三点共线,得
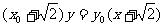 …………③ …………1分
…………③ …………1分
由A2、Q、M三点共线,得
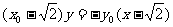 …………④ …………1分
…………④ …………1分
联立③、④,解得 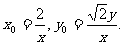 …………1分
…………1分
∵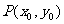 在双曲线上,
在双曲线上,
∴
∴轨迹E的方程为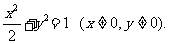 …………1分
…………1分
(Ⅲ)容易验证直线l的斜率不为0。
故可设直线l的方程为
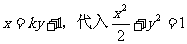 中,得
中,得

设 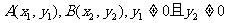
则由根与系数的关系,得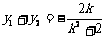 ……⑤
……⑤
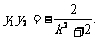 ……⑥ …………2分
……⑥ …………2分
∵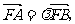 ∴有
∴有
将⑤式平方除以⑥式,得
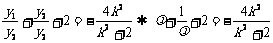 …………1分
…………1分
由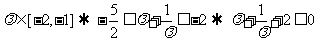
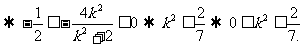 …………1分
…………1分
∵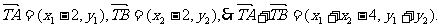
又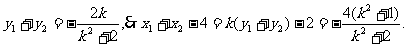
故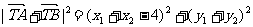
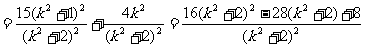
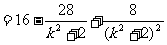
令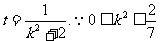 ∴
∴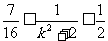 ,即
,即 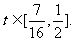
∴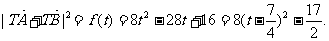
而 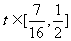 , ∴
, ∴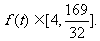
∴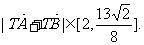
19、(北京市宣武区2008年高三综合练习二)已知椭圆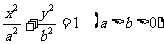 的离心率为,且其焦点F(c,0)(c>0)到相应准线l的距离为3,过焦点F的直线与椭圆交于A、B两点。
的离心率为,且其焦点F(c,0)(c>0)到相应准线l的距离为3,过焦点F的直线与椭圆交于A、B两点。
(1)求椭圆的标准方程;
(2)设M为右顶点,则直线AM、BM与准线l分别交于P、Q两点,(P、Q两点不重合),求证: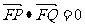
解:(1)由题意有 解得
解得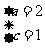
∴椭圆的标准方程为
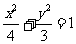 ……………………………………5分
……………………………………5分
(2)①若直线AB与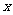 轴垂直,则直线AB的方程是
轴垂直,则直线AB的方程是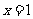
∵该椭圆的准线方程为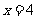 ,
,
∴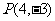 ,
,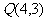 ,
∴
,
∴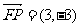 ,
,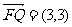
∴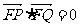 ∴当直线AB与
∴当直线AB与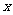 轴垂直时,命题成立。
轴垂直时,命题成立。
②若直线AB与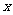 轴不垂直,则设直线AB的斜率为
轴不垂直,则设直线AB的斜率为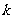 ,
,
∴直线AB的方程为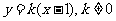
又设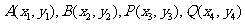
联立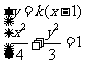 消y得
消y得 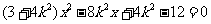
∴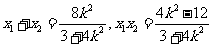 ∴
∴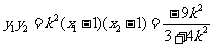
又∵A、M、P三点共线,∴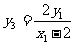 同理
同理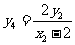
∴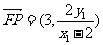 ,
,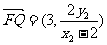
∴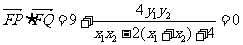
综上所述: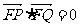
18、 (北京市宣武区2008年高三综合练习一)在面积为9的
(北京市宣武区2008年高三综合练习一)在面积为9的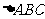 中,
中,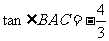 ,且
,且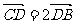 。现建立以A点为坐标原点,以
。现建立以A点为坐标原点,以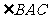 的平分线所在直线为x轴的平面直角坐标系,如图所示。
的平分线所在直线为x轴的平面直角坐标系,如图所示。
(1)求AB、AC所在的直线方程;
(2)求以AB、AC所在的直线为渐近线且过点D的双曲线的方程;
(3)过D分别作AB、AC所在直线的垂线DF、DE(E、F为垂足),求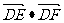 的值。
的值。
解:(1)设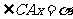
则由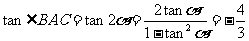

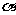 为锐角,
为锐角,
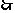
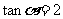 ,
,
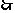 AC所在的直线方程为y=2x
AC所在的直线方程为y=2x
AB所在的直线方程为y= -2x…………………………………………….4分
(2)设所求双曲线为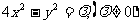
设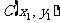 ,
,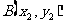 ,
,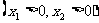 ,
,
由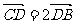 可得:
可得: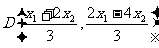
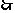
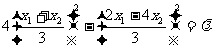 ,
,
即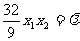
由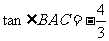 ,可得
,可得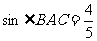 ,
,
又
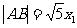 ,
,
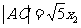 ,
,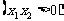
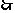
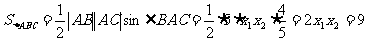 ,
,
即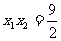 ,代入(1)得
,代入(1)得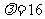 ,
,
双曲线方程为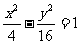 …………………………………………………9分
…………………………………………………9分
(3)由题设可知,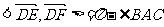 ,
,
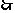
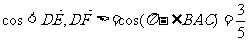
设点D为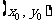 ,则
,则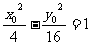
又点D到AB,AC所在直线距离
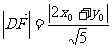 ,
,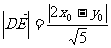 ,
,
而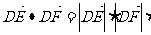
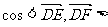 =
=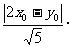
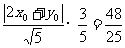
17、(北京市西城区2008年5月高三抽样测试)已知抛物线的方程为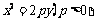 ,过点
,过点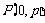 的直线
的直线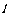 与抛物线相交于A、B两点,分别过点A、B作抛物线的两条切线
与抛物线相交于A、B两点,分别过点A、B作抛物线的两条切线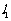 和
和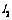 的斜率之积为定值;
的斜率之积为定值;
(Ⅰ)证明:直线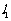 和
和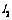 的斜率之积为定值;
的斜率之积为定值;
(Ⅱ)求点M的轨迹方程。
解:(I)依题意,直线l的斜率存在,设直线l的方程为y=kx+p

16、(北京市西城区2008年4月高三抽样测试)已知定点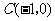 及椭圆
及椭圆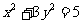 ,过点
,过点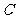 的动直线与椭圆相交于
的动直线与椭圆相交于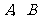 两点.
两点.
(Ⅰ)若线段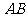 中点的横坐标是
中点的横坐标是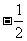 ,求直线
,求直线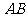 的方程;
的方程;
(Ⅱ)在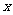 轴上是否存在点
轴上是否存在点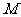 ,使
,使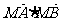 为常数?若存在,求出点
为常数?若存在,求出点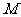 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(Ⅰ)解:
依题意,直线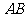 的斜率存在,设直线
的斜率存在,设直线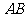 的方程为
的方程为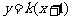 ,
,
将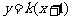 代入
代入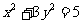 ,
消去
,
消去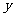 整理得
整理得
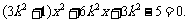 ………….. 2分
………….. 2分
设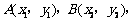 则
则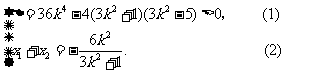 ………….. 4分
………….. 4分
由线段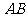 中点的横坐标是
中点的横坐标是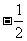 , 得
, 得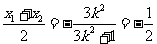 ,
,
解得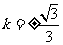 ,适合
,适合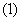 .
………….. 5分
.
………….. 5分
所以直线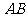 的方程为
的方程为
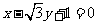 ,或
,或
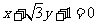 .
………….. 6分
.
………….. 6分
(Ⅱ)解:
假设在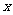 轴上存在点
轴上存在点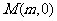 ,使
,使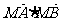 为常数.
为常数.
① 当直线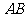 与
与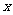 轴不垂直时,由(Ⅰ)知
轴不垂直时,由(Ⅰ)知 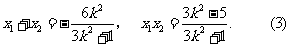
所以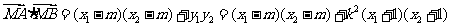
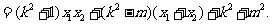 …………..
8分
…………..
8分
将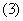 代入,整理得
代入,整理得
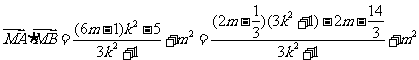
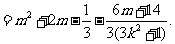
注意到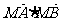 是与
是与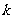 无关的常数,
从而有
无关的常数,
从而有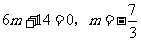 ,
此时
,
此时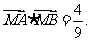 .. 11分
.. 11分
② 当直线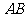 与
与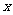 轴垂直时,此时点
轴垂直时,此时点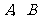 的坐标分别为
的坐标分别为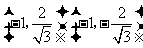 ,
,
当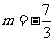 时,
亦有
时,
亦有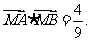 ………….. 13分
………….. 13分
综上,在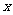 轴上存在定点
轴上存在定点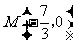 ,使
,使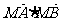 为常数.
为常数.
15、(北京市十一学校2008届高三数学练习题)如图,椭圆的中心在原点,其左焦点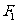 与抛物线
与抛物线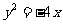 的焦点重合,过
的焦点重合,过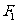 的直线
的直线 与椭圆交于A、B两点,与抛物线交于C、D两点.当直线
与椭圆交于A、B两点,与抛物线交于C、D两点.当直线 与x轴垂直时,
与x轴垂直时,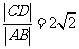 .
.
(Ⅰ)求椭圆的方程;
(II)求过点O、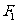 ,并且与椭圆的左准线相切的圆的方程;
,并且与椭圆的左准线相切的圆的方程;
(Ⅲ)求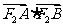 的最大值和最小值.
的最大值和最小值.
解:(Ⅰ)由抛物线方程,得焦点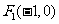 .
.
设椭圆的方程: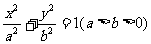 .
.
解方程组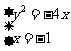 得C(-1,2),D(1,-2).
得C(-1,2),D(1,-2).
由于抛物线、椭圆都关于x轴对称,
∴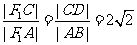 ,
,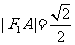 ,
∴
,
∴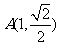 . …………2分
. …………2分
∴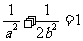 又
又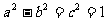 ,
,
因此,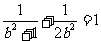 ,解得
,解得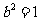 并推得
并推得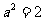 .
.
故椭圆的方程为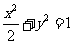 .
…………4分
.
…………4分
(Ⅱ)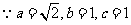 ,
,
 圆过点O、
圆过点O、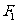 ,
,
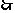 圆心M在直线
圆心M在直线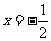 上.
上.
设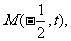 则圆半径,由于圆与椭圆的左准线相切,
则圆半径,由于圆与椭圆的左准线相切,
∴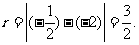
由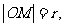 得
得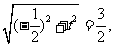 解得
解得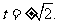
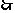 所求圆的方程为
所求圆的方程为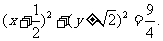 …………………………8分
…………………………8分
(Ⅲ) 由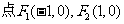
①若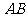 垂直于
垂直于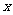 轴,则
轴,则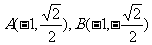 ,
,
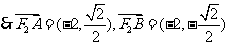 ,
,
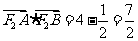 …………………………………………9分
…………………………………………9分
②若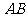 与
与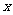 轴不垂直,设直线
轴不垂直,设直线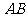 的斜率为
的斜率为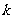 ,则直线
,则直线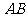 的方程为
的方程为
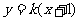
由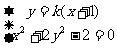 得
得 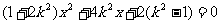
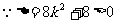 ,
,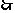 方程有两个不等的实数根.
方程有两个不等的实数根.
设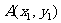 ,
,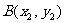 .
.
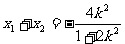 ,
, 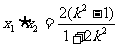 ………………………………11分
………………………………11分
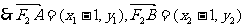
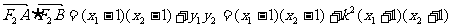

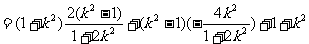
=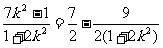
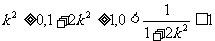
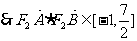 ,所以当直线
,所以当直线 垂于
垂于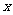 轴时,
轴时,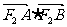 取得最大值
取得最大值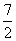
当直线 与
与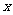 轴重合时,
轴重合时,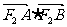 取得最小值
取得最小值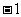
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com