
2.空间直线的位置关系:
板书:

板书:
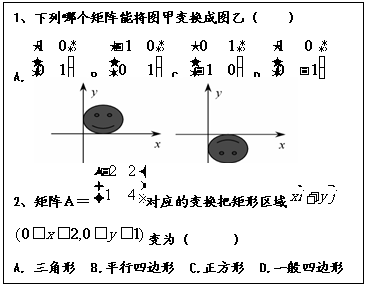
2、矩阵A=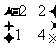 对应的变换把矩形区域
对应的变换把矩形区域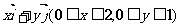 变为( )
变为( )
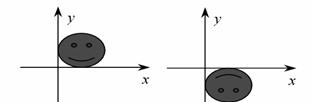
A. 三角形 B.平行四边形 C.正方形 D.一般四边形。
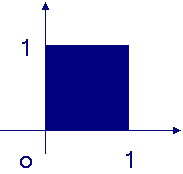
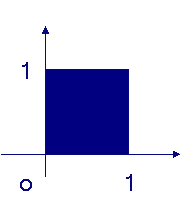
1、下列哪个矩阵能将图甲变换成图乙( )
A.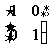 B.
B.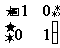 C.
C.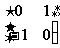 D.
D.
2、课堂演练
例1. 旋转变换: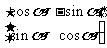
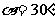 对应的矩阵A把单位正方形区域变成了什么图形?请画出图形。
对应的矩阵A把单位正方形区域变成了什么图形?请画出图形。

练习.下列切变变换对应的矩阵把A把单位正方形区域变成了什么图形?请画出图形。(同桌合作探究)
(1) (2)
(2) 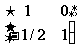

变式训练(任选1题)
本节课的整体思路是,课上通过精心设计的问题引导学生思考,通过师生的互动调动学生的积极性并观察学生的反馈,之后再利用合作探究以及改编题目进行变式训练来及时反馈学生的掌握情况。
本节课的引入是比较容易吸引学生眼球的一个生活例子,但是紧接着有一段推理会显得比较枯燥,需要的思维活动量较大,学生很容易在这里就昏昏欲睡了。这时采用精心设计的问题串来推波助澜,问题串的难度层次性较强,我们可以根据不同问题的难易程度,提问不同程度的学生,一方面调动整个班学生思考的积极性,一方面可以观察学生的反应来调整速度和难度。其中,课件的辅助作用是推理过程中的一个小亮点,希望通过动态的演示更直观地来帮助学生更快地找到答案。进入例题之后,记得跟引入呼应,学生会觉得本节课的可操作性还是比较强的,特别是进入合作探究,学生终于尝到了解决问题的甜头,而我们的目标也算比较好地得到了实现。




 引入环节
引入环节
 |
|||
|
|||



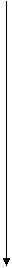


|








|





|


|
 |
|||||||||
 |
|||||||||
 |
|||||||||
 |
|||||||||
|




附: 《矩阵与变换》--线性变换的基本性质(二)学案
1、课前热身:(课前布置给学生去完成)
1)平面向量基本定理: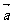 与
与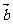 不共线,则对于平面内任何向量
不共线,则对于平面内任何向量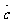 ,有且只有一对实数
,有且只有一对实数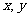 可由
可由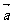 、
、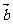 唯一表示成 :;其中不共线的向量
唯一表示成 :;其中不共线的向量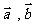 叫做表示这一平面内所有向量的一组_
_。
叫做表示这一平面内所有向量的一组_
_。
2)复习五种常见线性变换所对应矩阵
① 恒等变换: ② 旋转变换Ra ③ 切变变换: (平行于x轴,平行于y轴)
④ 反射变换:(关于x轴,关于y轴) ⑤ 投影变换: (投影到x轴,投影到y轴)
3)线性变换的基本性质:①数乘结合律: ;②分配律:___________________

4)点A(1,0)在矩阵P= 的作用下变成了什么?
5)过点M(1,0),N(0,2)的直线的向量形式可写成;在矩阵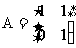 的作用下变成了什么图形?
的作用下变成了什么图形?
第一, 本节课设计知识点非常多,甚至有些知识点是2年前学习的,比如 平面向量基本定理,因此有必要让学生提前对这些知识点进行复习。
第二, 本节课只有一课时,却长达十页之多,全部纳入课堂是不可能的,为了不让学生感觉整块内容被拆得七零八落,必然要精挑细选。其中,几种常见的线性变换,旋转变换是比较形象的一种,我选择用它做例题,而切变变换是比较难理解的一种,我选择它来供学生进行探究。
第三, 我班学生思维不错,但学习主动性较差,结合上述第一二点,我打算设计一个学案(附后),包含了需要用到的知识点、课堂练习及课后作业。
学案课前热身是要课前布置给学生去完成的,包含了:
1)平面向量基本定理、五种常见线性变换对应矩阵、线性变换的基本性质
2)点A(1,0)在矩阵P=  的作用下变成了什么?
的作用下变成了什么?
3)过点M(1,0),N(0,2)的直线的向量形式可写成_________;在矩阵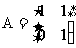 的作用下变成了什么图形?
的作用下变成了什么图形?
教法:问题驱动式教学,寻找学生思维的“最近发展区”通过联系旧知识,层层递进探寻新知,帮助学生找到解决新问题的方法。
学法:探究式学习方法,学生通过思考,归纳,合作探究进行学习,并鼓励学生课后进行Excel实践操作加深对矩阵与变换的对应关系的理解。
重点:让学生了解如何利用矩阵对单位正方形区域进行常见线性变换
难点:经历探究平行四边形区域向量形式的过程
知识目标:让学生探究出平行四边形区域的向量形式,了解如何利用矩阵对单位正方形区域进行常见线性变换,并通过平面图形帮学生更直观地巩固几种常见线性变换及其对应矩阵。
能力目标:能够运用所学的方法,利用矩阵对单位正方形区域进行常见的线性变换,更直观地体会矩阵与变换之间的对应关系,提高运用数形结合思想解决问题的能力。
情感目标:用最贴近生活的例子切入课题并逐步深入解决问题,充分激发学生学习数学的热情,让学生近距离地体验数学的“神奇”与“有用”。
选修4-2是一本非常新的教材,内容为《矩阵与变换》,是新课标新提出来的一个模块,旧教材是没有的。新课改将矩阵这一高等代数中占据着重要地位的概念在高中阶段提出来,无疑将高中的代数知识学习又上升到一个新的高度。对于这一模块的处理,各个版本教材有不少差异。福建省选用的是人教A版教材,对于代数中占据重要地位的矩阵,人教A版教材选择从变换的角度去切入,降低了高中生学习矩阵的门槛,同时又增强了矩阵的“直观性”和“趣味性”。本节课在本教材中的地位和作用分析如下:
从内容角度分析:自从矩阵与向量的乘法让我们实现了矩阵对点即向量的变换,从点到线,从线再到平面,从平面几何的概念来讲,乃一脉相承,几种线性变换与矩阵的联系得到了更形象的增强,平面图形的丰富性必然会让矩阵的“直观性”更具冲击力。该节课看似不是重点,却是一个知识的交汇点,起着承上启下的重要作用。
从思想角度分析:数形结合思想是高中阶段非常重要的思想,在新课改之前,这种思想可能更多地体现在诸如解析几何等内容。而利用矩阵这个代数工具来实现线性变换对平面区域的作用,可以说是将数形结合的思想推向了一个新的高度,让孩子们可以发自内心地去感叹“数学真的是有用的”。
从成长角度分析:该节课中所举的例子,有着浓厚的应用味道,充分符合课改中数学是“好玩”的精神,贴近生活的应用,可以让孩子们可以充分感受数学的无处不在,也可以让孩子们对接下去乃至大学高等代数的学习兴趣倍增,让他们的高数学习更加如鱼得水。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com