
8. (2008年上海理17)(13’)
(2008年上海理17)(13’)
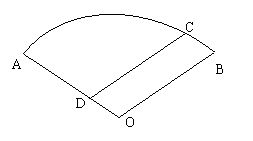
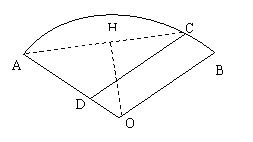
如图,某住宅小区的平面图呈圆心角为120°
的扇形AOB,小区的两个出入口设置在点A及点C
 处,且小区里有一条平行于BO的小路CD,已知某
处,且小区里有一条平行于BO的小路CD,已知某
人从C沿CD走到D用了10分钟,从D沿DA走到A
用了6分钟,若此人步行的速度为每分钟50米,
求该扇形的半径OA的长(精确到1米)
[解析][解法一] 设该扇形的半径为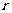 米,连接
米,连接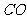 . ……2分
. ……2分
由题意,得 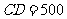 (米),
(米),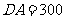 (米),
(米),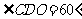 ……4分
……4分
在△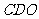 中,
中,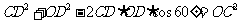 ……6分
……6分
即,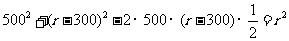 ……9分
……9分
解得 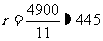 (米)答:该扇形的半径
(米)答:该扇形的半径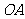 的长约为445米. ……13分
的长约为445米. ……13分
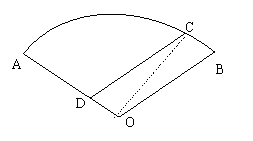
 [解法二] 连接
[解法二] 连接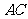 ,作
,作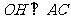 ,交
,交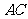 于
于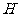 , ……2分
, ……2分
由题意,得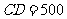 (米),
(米),
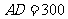 (米),
(米),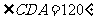 ……4分
……4分
在△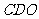 中,
中,
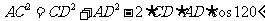
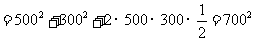 .
.
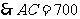 (米).
……6分
(米).
……6分
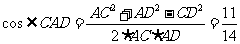 . ……9分
. ……9分
在直角△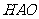 中,
中,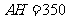 (米),
(米),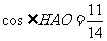 ,
,
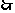
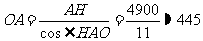 (米).
(米).
答:该扇形的半径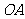 的长约为445米. ……13分
的长约为445米. ……13分
6.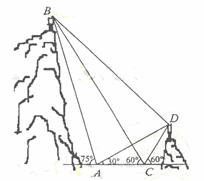 (2009年辽宁理 17 ) (本小题满分 12 分)
(2009年辽宁理 17 ) (本小题满分 12 分)
如图, A , B , C , D 都在同一个与水平面垂直的平面内, B , D 为两岛上的两座灯塔的塔顶.测量船于水面A处测得 B 点和 D 点的仰角分别为750 , 300 ,于水面C处测得B点和D点的仰角都为600,AC=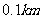 .试探究图中B,D间距离与另外哪两点距离相等,然后求B,D 的距离 (计算结果精确到
.试探究图中B,D间距离与另外哪两点距离相等,然后求B,D 的距离 (计算结果精确到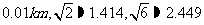 )
)
解:在△ACD中,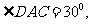
 所以CD=
AC=
所以CD=
AC=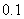 .
.
又∠BCD=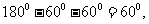 故CB是△CAD底边的中垂线,所以BD=BA。--5 分
故CB是△CAD底边的中垂线,所以BD=BA。--5 分
在△ABC中,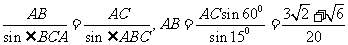 ,因此,
,因此,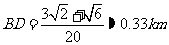 ,故B,D 的距离为
,故B,D 的距离为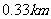 。--------------12 分
。--------------12 分
|
在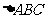 中,角
中,角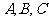 所对的边分别为
所对的边分别为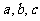 ,且满足
,且满足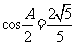 ,
, .
.
(I)求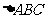 的面积; (II)若
的面积; (II)若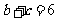 ,求
,求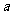 的值.
的值.
解析:(I)因为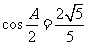 ,
,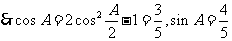 ,
,
又由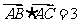 ,得
,得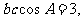
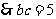 ,
,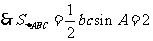
(II)对于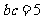 ,又
,又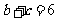 ,
,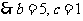 或
或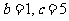 ,
,
由余弦定理得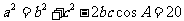 ,
,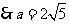
5.(2009年安徽理16)(本小题满分12分)
在 ABC中,
ABC中,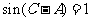 , sinB=
, sinB=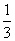 .
.
(I)求sinA的值;
(II)设AC=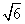 ,求
,求 ABC的面积.
ABC的面积.
本小题主要考查三角恒等变换、正弦定理、解三角形等有关知识,考查运算求解能力。本小题满分12分
解:(Ⅰ)由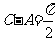 ,且
,且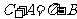 ,∴
,∴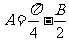 ,∴
,∴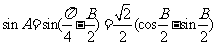 ,
,
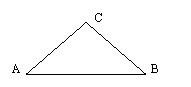 ∴
∴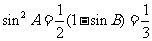 ,又
,又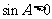 ,∴
,∴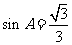
(Ⅱ)如图,由正弦定理得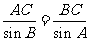
∴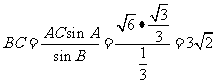 ,又
,又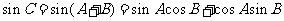
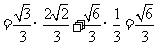 ∴
∴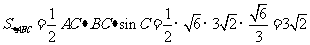


4.(2009年天津理17)(本小题满分12分)
在⊿ABC中,BC=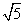 ,AC=3,sinC=2sinA
,AC=3,sinC=2sinA
(I) 求AB的值: (II) 求sin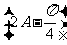 的值
的值
解析:本小题主要考查正弦定理、余弦定理、同角三角函数的基本关系、二倍角的正弦与余弦、两角差的正弦等基础知识,考查基本运算能力。满分12分。
(Ⅰ)解:在△ABC中,根据正弦定理,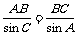 于是AB=
于是AB=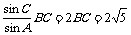
(Ⅱ)解:在△ABC中,根据余弦定理,得cosA=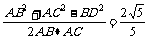
于是 sinA=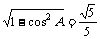 从而sin2A=2sinAcosA=
从而sin2A=2sinAcosA=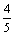 ,cos2A=cos2A-sin2A=
,cos2A=cos2A-sin2A=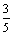
所以 sin(2A-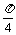 )=sin2Acos
)=sin2Acos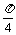 -cos2Asin
-cos2Asin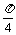 =
=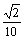
3.(2009年海南理17)(本小题满分12分)
为了测量两山顶M,N间的距离,飞机沿水平方向在A,B两点进行测量,A,B,M,N在同一个铅垂平面内(如示意图),飞机能够测量的数据有俯角和A,B间的距离,请设计一个方案,包括:①指出需要测量的数据(用字母表示,并在图中标出);②用文字和公式写出计算M,N间的距离的步骤。
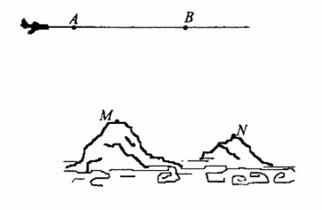
解:方案一:①需要测量的数据有:A点到M,N点的俯角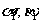 ;B点到M,
;B点到M,
N的俯角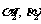 ;A,B的距离 d (如图所示) .
;A,B的距离 d (如图所示) .
②第一步:计算AM . 由正弦定理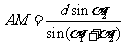 ;
;
第二步:计算AN . 由正弦定理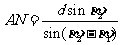 ;
;
第三步:计算MN. 由余弦定理 .
.
方案二:①需要测量的数据有:
A点到M,N点的俯角 ,
,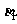 ;B点到M,N点的府角
;B点到M,N点的府角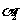 ,
,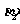 ;A,B的距离 d (如图所示).
;A,B的距离 d (如图所示).
②第一步:计算BM . 由正弦定理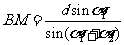 ;
;
第二步:计算BN . 由正弦定理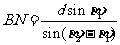 ;
;
第三步:计算MN . 由余弦定理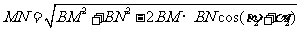
2.(2010年福建理19)(本小题满分13分)
 。
。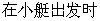 ,轮船位于港口O北偏西
,轮船位于港口O北偏西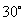 且与该港口相距20海里的A处,并以30海里/小时的航行速度沿正东方向匀速行驶。假设该小船沿直线方向以
且与该港口相距20海里的A处,并以30海里/小时的航行速度沿正东方向匀速行驶。假设该小船沿直线方向以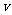 海里/小时的航行速度匀速行驶,经过t小时与轮船相遇。
海里/小时的航行速度匀速行驶,经过t小时与轮船相遇。
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向与航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由。
[解析]如图,由(1)得
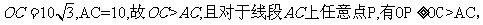 而小艇的最高航行速度只能达到30海里/小时,故轮船与小艇不可能在A、C(包含C)的任意位置相遇,设
而小艇的最高航行速度只能达到30海里/小时,故轮船与小艇不可能在A、C(包含C)的任意位置相遇,设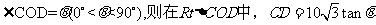 ,OD=
,OD=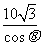 ,
,
由于从出发到相遇,轮船与小艇所需要的时间分别为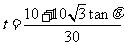 和
和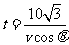 ,
,
所以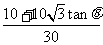
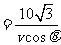 ,解得
,解得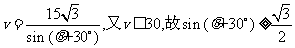 ,
,
从而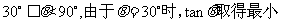 值,且最小值为
值,且最小值为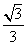 ,于是
,于是
当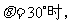
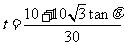 取得最小值,且最小值为
取得最小值,且最小值为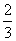 。
。
此时,在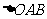 中,
中,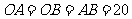 ,故可设计航行方案如下:
,故可设计航行方案如下:
航行方向为北偏东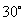 ,航行速度为30海里/小时,小艇能以最短时间与轮船相遇。
,航行速度为30海里/小时,小艇能以最短时间与轮船相遇。
1.( 2010年陕西理17)(本小题满分12分)
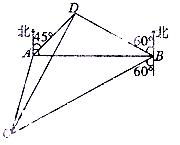
如图,A,B是海面上位于东西方向相距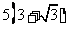 海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距
海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距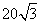 海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
 解: 由题意知AB=
解: 由题意知AB=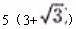 海里,
海里,
∠ DA B=90°-60°=30°,∠ DAB=90°-45°=45°,
B=90°-60°=30°,∠ DAB=90°-45°=45°,
∴∠ADB=180°-(45°+30°)=105°,
在△ADB中,有正弦定理得
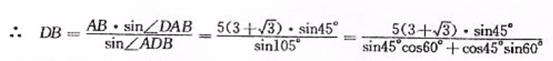
6.(2008年江苏13)满足条件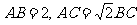 的三角形
的三角形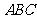 的面积的最大值
的面积的最大值
[解析]本小题考查三角形面积公式、余弦定理以及函数思想.设BC=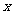 ,则AC=
,则AC=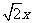 ,
,
根据面积公式得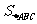 =
=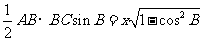 ,根据余弦定理得
,根据余弦定理得
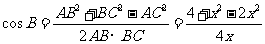
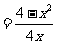 ,代入上式得
,代入上式得
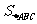 =
=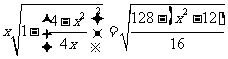 由三角形三边关系有
由三角形三边关系有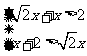
解得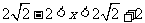 ,故当
,故当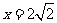 时取得
时取得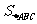 最大值
最大值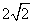 答案]
答案]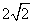
5.(2010年山东理15)在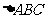 中,角
中,角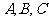 所对的边分别为a,b,c,若
所对的边分别为a,b,c,若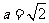 ,
,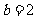 ,
,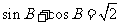 ,则角
,则角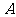 的大小为
的大小为  .
.
[答案]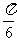 [解析]由
[解析]由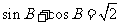 得
得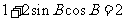 ,即
,即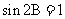 ,因为
,因为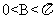 ,所以
,所以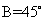 ,又因为
,又因为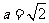 ,
,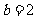 ,所以在
,所以在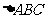 中,由正弦定理得:
中,由正弦定理得: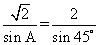 ,解得
,解得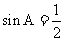 ,又
,又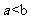 ,所以
,所以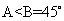 ,所以
,所以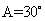 。
。
[命题意图]本题考查了三角恒等变换、已知三角函数值求解以及正弦定理,考查了同学们解决三角形问题的能力,属于中档题。
4..(2010年广东理11)已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b=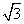 ,
A+C=2B,则sinC= .
,
A+C=2B,则sinC= .
解析由A+C=2B及A+ B+ C=180°知,B =60°.由正弦定理知,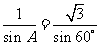 ,
,
即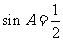 .由
.由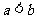 知,
知,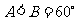 ,则
,则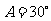 ,
,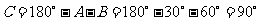 ,
,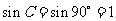 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com