
3.(2010年北京理10)在△ABC中,若b = 1,c =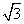 ,
,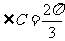 ,则a =
。
,则a =
。
解析: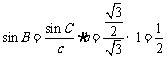 ,因此
,因此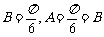 ,故
,故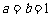
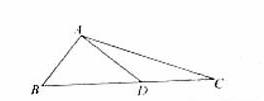
2.(2010年天津理15)如图,在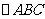 中,
中, ,
,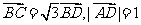 ,则
,则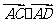 =
。
=
。

[答案]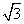
[解析]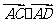 =
=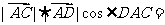
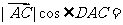
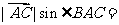
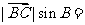
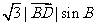 =
=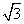 .
.
[命题意图]本题主要考查平面向量、解三角形等基础知识,考查化归与转化的数学思想,有点难度.
1. (2010年全国理16)在△ABC中,D为边BC上一点,BD=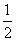 DC,
DC, ADB=120°,AD=2,若△ADC的面积为
ADB=120°,AD=2,若△ADC的面积为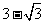 ,则
,则 BAC=_______
BAC=_______
[答案]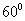 解析:设
解析:设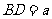 ,则
,则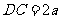 ,由已知条件有
,由已知条件有
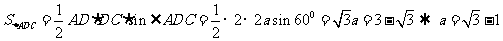 ,再由余弦定理分别得到
,再由余弦定理分别得到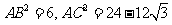 ,再由余弦定理得
,再由余弦定理得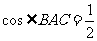 ,所以
,所以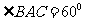 .
.
7.(2007年山东理11)在直角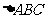 中,
中,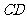 是斜边
是斜边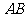 上的高,则下列等式不成立的是
上的高,则下列等式不成立的是
(A)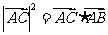 (B)
(B) 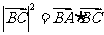
(C)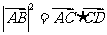 (D)
(D) 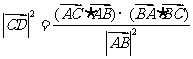
[答案]:C.[分析]: 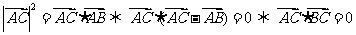 ,A是正确的,同理B也正确,对于D答案可变形为
,A是正确的,同理B也正确,对于D答案可变形为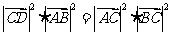 ,通过等积变换判断为正确.
,通过等积变换判断为正确.
6.(2008年海南理3)如果等腰三角形的周长是底边长的5倍,那么它的顶角的余弦值为
A.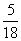 B.
B.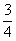 C.
C.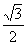 D.
D.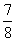
D解:设顶角为C,因为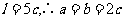 ,由余弦定理
,由余弦定理
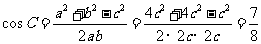
5.(2009年广东理6) 一质点受到平面上的三个力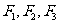 (单位:牛顿)的作用而处于平衡状态.已知
(单位:牛顿)的作用而处于平衡状态.已知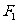 ,
,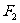 成
成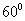 角,且
角,且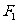 ,
,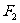 的大小分别为2和4,则
的大小分别为2和4,则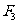 的大小为
的大小为
A. 6
B. 2 C.
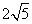 D.
D. 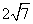
[解析]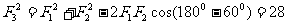 ,所以
,所以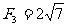 ,选D.
,选D.
4.( 2010年上海理18) 某人要制作一个三角形,要求它的三条高的长度分别为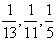 ,则此人能
,则此人能
(A)不能作出这样的三角形 (B)作出一个锐角三角形
(C)作出一个直角三角形 (D)作出一个钝角三角形
[答](D)解析:设三边分别为a,b,c,利用面积相等可知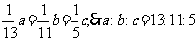
由余弦定理得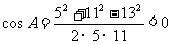 ,所以角A为钝角
,所以角A为钝角
3.(2010年辽宁理5)设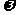 >0,函数y=sin(
>0,函数y=sin(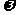 x+
x+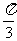 )+2的图像向右平移
)+2的图像向右平移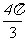 个单位后与原图像重合,则
个单位后与原图像重合,则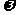 的最小值是
的最小值是
(A)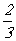 (B)
(B)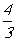 (C)
(C)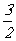 (D)3
(D)3
[答案]C[解析]将y=sin(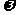 x+
x+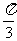 )+2的图像向右平移
)+2的图像向右平移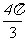 个单位后为
个单位后为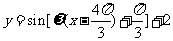
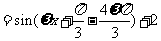 ,所以有
,所以有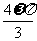 =2k
=2k ,即
,即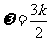 ,又因为
,又因为 ,所以k≥1,故
,所以k≥1,故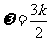 ≥
≥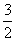 ,所以选C
,所以选C
2.( 2010年湖南理6)在△ABC中,角A,B,C所对的边长分别为a,b,c,若∠C=120°,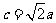 ,则( )
,则( )
A、a>b B、a<b C、a=b D、a与b的大小关系不能确定
1.(2010年天津理7)在△ABC中,内角A、B、C的对边分别是a、b、c,若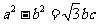 ,sinC=
,sinC= 2
2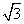 sinB,则A=
sinB,则A=
(A)30° (B)60° (C)120° (D)150°
[答案]A[解析]由sinC= 2
2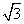 sinB结合正弦定理得:
sinB结合正弦定理得: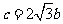 ,所以由于余弦定理得:
,所以由于余弦定理得:
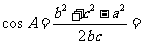
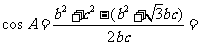
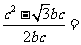
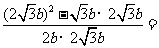
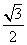 ,所以A=30°,选A。
,所以A=30°,选A。
[命题意图]本小题考查三角形中的正弦定理、余弦定理,特殊角的三角函数等基础知识,考查同学们的运算能力。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com