22.　 解：1. 记“从中一次摸出两个球，两球恰好颜色不同”为事件A则P(A)=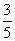

21.解：因为该点在圆外设直线斜率为K则方程为y-4=k(x-2)即kx-y+4-2k=0所以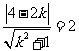解得K＝所以直线方程为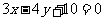：或

20.1解：记“点数之和为8”为事件A则P(A)=.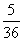

2记“点数之和大于10”为事件B则P(B)=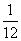

19.解：设所求圆的方程为：(x+3)²+y²－13+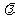(x²+(y+3)²－37)＝0

因为圆心在x-y-4=0上，所以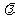＝－7所以圆方程是：

3.　 记“所选3人至少有1名女生”为事件C则其对立事件为A事件则P(C)=

21. 求过点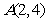向圆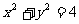所引的切线方程。

22一个口袋内装有大小相同的2个白球和3个黑球．

(Ⅰ)从中一次摸出两个球，求两球恰好颜色不同的概率；

(Ⅱ)从中摸出一个球，放回后再摸出一个球，求两球同时是黑球的概率；

(Ⅲ)从中摸出一个球，放回后再摸出一个球，求两球恰好颜色不同的概率．

.2记“所选3人恰有1名女生”为事件B则　　　　　　　　　　　　　　　　　　　　　　　　 P(B)=

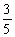
20．将一颗骰子连掷两次.

(1)　 求点数之和为8的概率.

(2)　 求点数之和大于10的概率.

19．求经过两圆(x+3)²+y²=13和x²+(y+3)²=37的交点，且圆心在直线x－y－4=0上的圆的方程.

18．从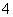名男生和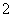名女生中任选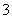人参加演讲比赛,

①求所选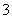人都是男生的概率;

②求所选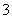人恰有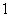名女生的概率;

③求所选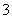人中至少有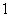名女生的概率　

17．求以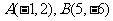为直径两端点的圆的方程。