
(一)填空题:
1、(07浙江)随机变量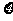 的分布列如下:
的分布列如下:
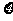
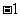
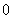
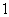
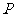
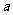
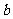
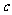
其中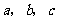 成等差数列,若
成等差数列,若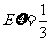 ,则
,则 的值是
;
的值是
;
2、(07福建)两封信随机投入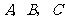 三个空邮箱,则
三个空邮箱,则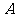 邮箱的信件数
邮箱的信件数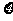 的数学期望
的数学期望
;
3、(06四川)设离散型随机变量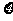 可能取的值为1,2,3,4.
可能取的值为1,2,3,4.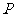 (
(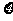 =
=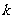 )=
)=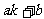 (
(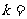 1,2,3,4),又
1,2,3,4),又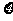 的数学期望
的数学期望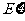 =3,则
=3,则 =______________。
=______________。
例1、(07山东)设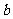 和
和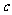 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量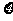 表示方程
表示方程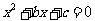 实根的个数(重根按一个计).(Ⅰ)求方程
实根的个数(重根按一个计).(Ⅰ)求方程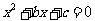 有实根的概率;
有实根的概率;
(Ⅱ)求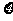 的分布列和数学期望;(Ⅲ)求在先后两次出现的点数中有5的条件下,方程
的分布列和数学期望;(Ⅲ)求在先后两次出现的点数中有5的条件下,方程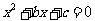 有实根的概率.
有实根的概率.
例2、(07海南20理) 如图,面积为
如图,面积为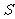 的正方形
的正方形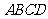 中有一个不规则的图形
中有一个不规则的图形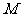 ,可按下面方法估计
,可按下面方法估计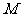 的面积:在正方形
的面积:在正方形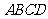 中随机投掷
中随机投掷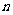 个点,若
个点,若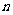 个点中有
个点中有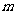 个点落入
个点落入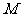 中,则
中,则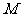 的面积的估计值为
的面积的估计值为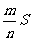 ,假设正方形
,假设正方形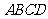 的边长为2,
的边长为2,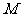 的面积为1,并向正方形
的面积为1,并向正方形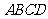 中随机投掷
中随机投掷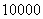 个点,以
个点,以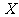 表示落入
表示落入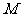 中的点的数目.
中的点的数目.
(I)求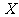 的均值
的均值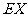 ;
;
(II)求用以上方法估计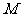 的面积时,
的面积时,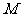 的面积的估计值与实际值之差在区间
的面积的估计值与实际值之差在区间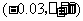 内的概率.
内的概率.
附表: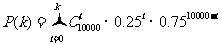
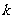
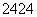
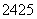
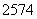
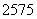
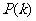
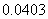
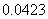
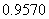
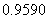
解:每个点落入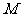 中的概率均为
中的概率均为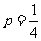 .
.
依题意知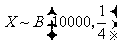 .
.
(Ⅰ)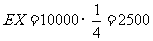 .
.
(Ⅱ)依题意所求概率为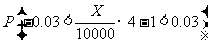 ,
,
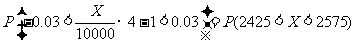
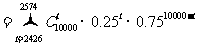
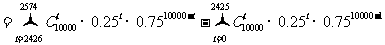
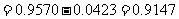 .
.
例3、(06全国Ⅰ)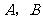 是治疗同一种疾病的两种药,用若干试验组进行对比试验。每个试验组由4只小白鼠组成,其中2只服用
是治疗同一种疾病的两种药,用若干试验组进行对比试验。每个试验组由4只小白鼠组成,其中2只服用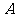 ,另2只服用
,另2只服用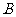 ,然后观察疗效。若在一个试验组中,服用
,然后观察疗效。若在一个试验组中,服用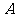 有效的小白鼠的只数比服用
有效的小白鼠的只数比服用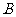 有效的多,就称该试验组为甲类组。设每只小白鼠服用
有效的多,就称该试验组为甲类组。设每只小白鼠服用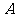 有效的概率为
有效的概率为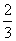 ,服用
,服用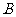 有效的概率为
有效的概率为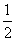 。(Ⅰ)求一个试验组为甲类组的概率;(Ⅱ)观察3个试验组,用
。(Ⅰ)求一个试验组为甲类组的概率;(Ⅱ)观察3个试验组,用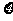 表示这3个试验组中甲类组的个数,求
表示这3个试验组中甲类组的个数,求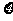 的分布列和数学期望。
的分布列和数学期望。
例4、(06广东)某运动员射击一次所得环数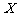 的分布如下:
的分布如下:
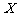 |
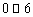 |
7 |
8 |
9 |
10 |
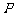 |
0 |
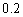 |
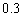 |
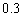 |
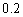 |
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为 .
.
(I)求该运动员两次都命中7环的概率;
(II)求 的分布列;
的分布列;
(III) 求 的数学期望
的数学期望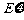 。
。
(三)解答题:
(二)填空题:
(一)选择题:
例(07广东17)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量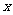 (吨)与相应的生产能耗
(吨)与相应的生产能耗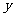 (吨标准煤)的几组对照数据.
(吨标准煤)的几组对照数据.
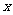 |
3 |
4 |
5 |
6 |
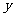 |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出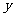 关于
关于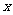 的线性回归方程
的线性回归方程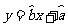 ;
;
(3)已知该厂技改前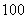 吨甲产品的生产能耗为
吨甲产品的生产能耗为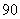 吨标准煤.试根据(2)求出的线性回归方程,预测生产
吨标准煤.试根据(2)求出的线性回归方程,预测生产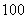 吨甲产品的生产能耗比技改前降低多少吨标准煤?
吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值: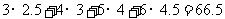 )
)
解析:
(1) 略;
(2) 方法1(不作要求):设线性回归方程为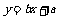 ,则
,则
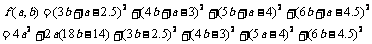
∴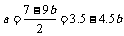 时,
时,
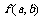 取得最小值
取得最小值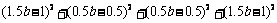
即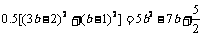 ,∴
,∴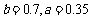 时f(a,b)取得最小值;
时f(a,b)取得最小值;
所以线性回归方程为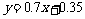 ;
;
方法2:由系数公式可知,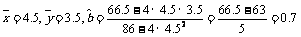
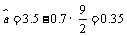 ,所以线性回归方程为
,所以线性回归方程为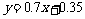 ;
;
(3)x=100时,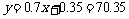 ,所以预测生产100吨甲产品的生产能耗比技术改造前降低19.65吨标准煤.
,所以预测生产100吨甲产品的生产能耗比技术改造前降低19.65吨标准煤.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com