
3.有一家父母得知其小孩在外偷了东西,如果他们相信荀子的理论,可能对小孩采取的态度是( )
A.认为孩子的本性是恶的,但只要好好教育,孩子会改正错误
B.认为孩子的本性是善的,他犯错误是一时糊涂
C.认为孩子的本性是恶的,必须严厉地惩罚他,使他害怕,以防再犯
D.认为孩子犯错本性造成,而是环境不好,应择善而居
2.西汉时,一大夫随武帝外出打猎,武帝猎得一头小鹿,交大夫带回,路遇母鹿,两鹿相互哀鸣,引起大夫的恻隐之心,便放了小鹿。董仲舒断曰:“中感母恩,虽废君命,徒之可也。”既大夫胸怀母爱之情,虽然有违君命,但也应减轻处罚。董仲舒的断案体现的思想是 ( )
A.“兼爱” B.“以仁入法” C.“心即理也” D.“致良知”
1.在他看来,“理想的臣民有粗大的骨骼、强壮的肌肉和空空如也的脑袋;而理想的统治者则是‘清心寡欲地治理人民……填饱肚子’”。“他”最有可能是 ( )
A.老子 B.孔子 C.荀子 D.韩非
21.解:(Ⅰ)由题意知,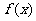 的定义域为
的定义域为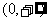 ,
… 1分
,
… 1分
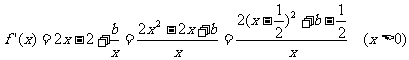 ………
2分
………
2分
∴当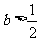 时,
时, 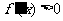 ,函数
,函数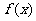 在定义域
在定义域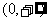 上单调递增. …3分
上单调递增. …3分
(Ⅱ)①由(Ⅰ)得,当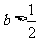 时,函数
时,函数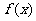 无极值点.
…… 4分
无极值点.
…… 4分
②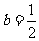 时,
时,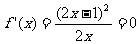 有两个相同的解
有两个相同的解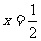 ,
,
但当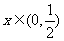 时,
时,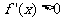 ,当
,当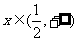 时,
时,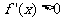
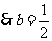 时,函数
时,函数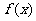 在
在 上无极值点.
………………5分
上无极值点.
………………5分
③当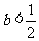 时,
时,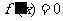 有两个不同解,
有两个不同解,
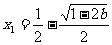
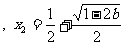
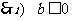 时,
时,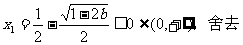 ,
,
而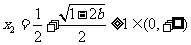 ,
,
此时
 ,
, 随
随 在定义域上的变化情况如下表:
在定义域上的变化情况如下表:
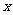 |
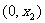 |
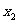 |
 |
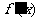 |
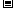 |
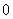 |
 |
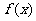 |
减 |
极小值 |
增 |
由此表可知:当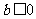 时,
时,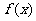 有惟一极小值点
有惟一极小值点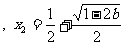 , ……
8分
, ……
8分
ii) 当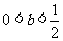 时,0<
时,0< <1
<1
此时,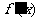 ,
,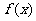 随
随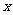 的变化情况如下表:
的变化情况如下表:
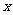 |
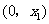 |
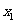 |
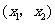 |
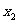 |
 |
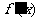 |
 |
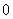 |
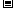 |
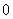 |
 |
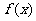 |
增 |
极大值 |
减 |
极小值 |
增 |
由此表可知: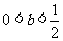 时,
时,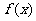 有一个极大值
有一个极大值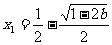 和一个极小值点
和一个极小值点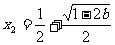 ;
………11分
;
………11分
综上所述:
当且仅当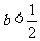 时
时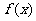 有极值点;
有极值点;
当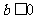 时,
时,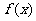 有惟一最小值点
有惟一最小值点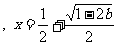 ;
;
当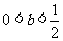 时,
时,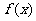 有一个极大值点
有一个极大值点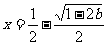 和一个极小值点
和一个极小值点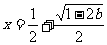 ………12分
………12分
20.解:(Ⅰ)由于点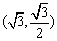 在椭圆上,
在椭圆上,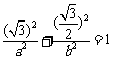 ……………………… 1分
……………………… 1分
2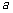 =4, ………………………2分
=4, ………………………2分
椭圆C的方程为 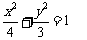 ………………………3分
………………………3分
焦点坐标分别为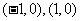 ………………………4分
………………………4分
(Ⅱ)设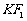 的中点为B(x, y)则点
的中点为B(x, y)则点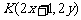 ………………………5分
………………………5分
把K的坐标代入椭圆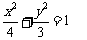 中得
中得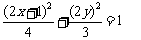 ………………7分
………………7分
线段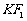 的中点B的轨迹方程为
的中点B的轨迹方程为 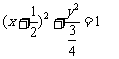 ………………8分
………………8分
(Ⅲ)过原点的直线L与椭圆相交的两点M,N关于坐标原点对称
设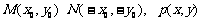
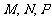 在椭圆上,应满足椭圆方程,得
在椭圆上,应满足椭圆方程,得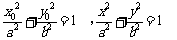 ………………10分
………………10分
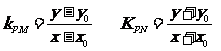 ………………11分
………………11分
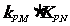 =
=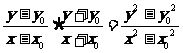 =
=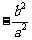 ………………13分
………………13分
故: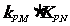 的值与点P的位置无关,同时与直线L无关,………………14分
的值与点P的位置无关,同时与直线L无关,………………14分
19.(Ⅰ)由程序框图可知: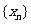 是等差数列,且首项
是等差数列,且首项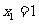 ,公差
,公差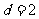
∴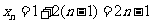 ………………………3分
………………………3分
(Ⅱ)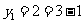 ,
,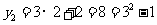 ,
,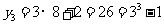
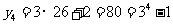
故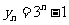 ………………………7分
………………………7分
(Ⅲ) 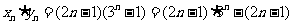

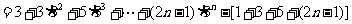

令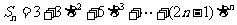
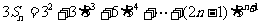
∴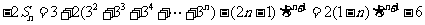
∴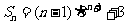
∴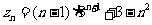 ………………………14分
………………………14分
18.解:
(Ⅰ)证明:
 平面
平面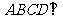 平面
平面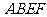 ,
,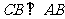 ,平面
,平面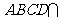 平面
平面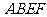 =
=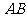
∴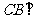 平面
平面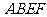
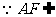 平面
平面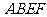
∴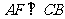
又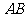 为圆
为圆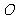 的直径
的直径
∴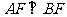
∴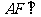 平面
平面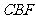 ……………………4分
……………………4分
(Ⅱ)设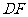 的中点为
的中点为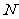 ,则
,则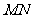
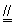
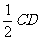
又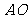
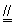
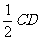 ,
,
∴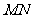
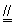
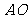
∴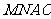 为平行四边形
为平行四边形
∴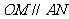
又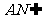 平面
平面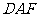 ,
,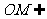 平面
平面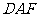
∴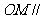 平面
平面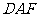 ………………………9分
………………………9分
(Ⅲ)过点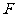 作
作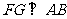 于
于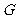
 平面
平面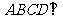 平面
平面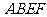 ,
,
∴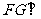 平面
平面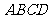 ,
, 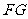 即正
即正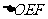 的高
………………………11分
的高
………………………11分
∴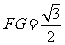
∴ 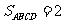
∴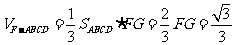 ………………………14分
………………………14分
17.解:(Ⅰ)由频率分布直方图知,成绩在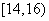 内的人数为:
内的人数为: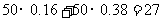 (人)
(人)
所以该班成绩良好的人数为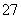 人. ……………………… 4分
人. ……………………… 4分
(Ⅱ)由频率分布直方图知,成绩在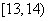 的人数为
的人数为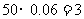 人,设为
人,设为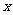 、
、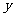 、
、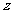 ;…… 5分
;…… 5分
成绩在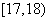 的人数为
的人数为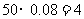 人,设为
人,设为 、
、 、
、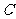 、
、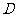 …… 6分
…… 6分
若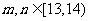 时,有
时,有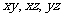
 种情况; ………………
8分
种情况; ………………
8分
若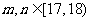 时,有
时,有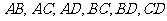
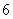 种情况;……………… 10分
种情况;……………… 10分
若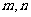 分别在
分别在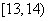 和
和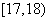 内时,
内时,
|
|
A |
B |
C |
D |
|
x |
xA |
xB |
xC |
xD |
|
y |
yA |
yB |
yC |
yD |
|
z |
zA |
zB |
zC |
zD |
共有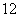 种情况.
种情况.
所以基本事件总数为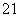 种,事件“
种,事件“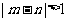 ”所包含的基本事件个数有
”所包含的基本事件个数有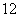 种。13分
种。13分
∴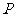 (
(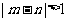 )
)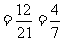 。
……………………… 14分
。
……………………… 14分
16.解:(Ⅰ)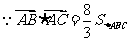
∴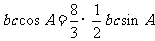
∴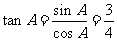
又 ,
,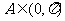
∴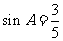 ……………………………… 6分
……………………………… 6分
()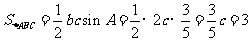 ∴
∴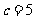
∵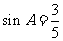 ∴
∴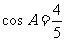
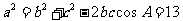
∴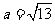 ……………………………… 12分
……………………………… 12分
15.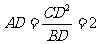 ,
,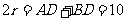 ,故
,故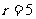 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com