
4.已知某种植物紫色和红色色素形成的生物化学途径是:
合成了红色中间产物就开红花,合成了紫色物质就开紫花,否则开白花。A基因和B基因分别位于两对染色体上
 ,基因型为AaBb的植株自交,子一代植株的表现型及比例为( A )
,基因型为AaBb的植株自交,子一代植株的表现型及比例为( A )
A.紫花∶红花∶白花=9∶3∶4 
B.紫花∶白花=1∶1 
C.紫花∶白花=9∶7 
D.紫花∶红花∶白花=9∶6∶1
3.一个基因型为Aa的杂合子豚鼠,一次产生了100万个精子,其中含有隐性遗传因子的精子数目为( )

A.100万个
B.50万个 C.25万个 D.0个

2.遗传因子组成为HH的绵羊有角,遗传因子组成为hh的绵羊无角,遗传因子组成为Hh的绵羊中,母羊无角,公羊有角。现有一头有角羊生了一头无角羊,则亲本公羊的遗传因子组成是( )

A.hh
B.Hh C.HH D.不能确定

1.下列性状中,不属于相对性状的是( )

A.猫的白毛和黑毛 B.人的卷发与直发 
C.人的五指与多指 D.人的大眼与双眼皮

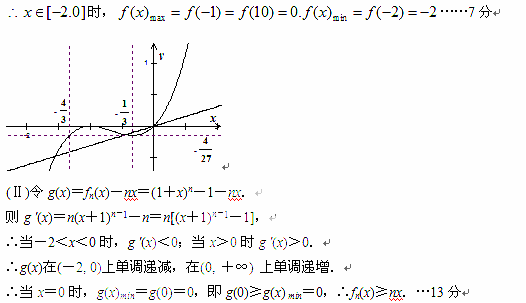
21.(Ⅰ)设
∴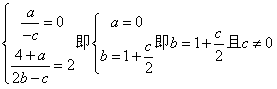 ………………………………2分
………………………………2分
(Ⅱ)∵c=2 ∴b=2
∴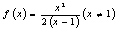 ,
,
由已知可得2Sn=an-an2……①,且an≠1.
当n≥2时,2 Sn -1=an-1-an-12 ……②,
①-②得(an+an-1)( an-an-1+1)=0,∴an=-an-1 或 an=-an-1 =-1,
当n=1时,2a1=a1-a12 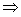 a1=-1,
a1=-1,
若an=-an-1,则a2=1与an≠1矛盾.∴an-an-1=-1, ∴an=-n.………………4分
∴要证待证不等式,只要证 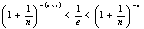 ,
,
即证 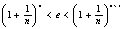 ,
,
只要证 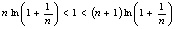 ,即证
,即证 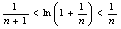 .
.
考虑证不等式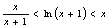 (x>0) **.…………………………………………………6分
(x>0) **.…………………………………………………6分
令g(x)=x-ln(1+x), h(x)=ln(x+1)-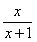 (x>0) .
(x>0) .
∴g '(x)=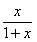 , h '(x)=
, h '(x)=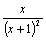 ,
,
∵x>0, ∴g '(x)>0, h '(x)>0,∴g(x)、h(x)在(0, +∞)上都是增函数,
∴g(x)>g(0)=0, h(x)>h(0)=0,∴x>0时,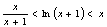 .
.
令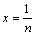 则**式成立,∴
则**式成立,∴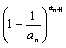 <
<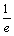 <
<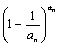 ,……………………………………9分
,……………………………………9分
(Ⅲ)由(Ⅱ)知bn=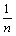 ,则Tn=
,则Tn=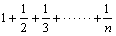 .
.
在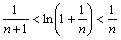 中,令n=1,2,3,……,2008,并将各式相加,
中,令n=1,2,3,……,2008,并将各式相加,
得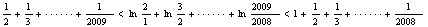 ,
,
即T2009-1<ln2009<T2008.…………………………………………………………………12分
20. (Ⅰ)依题设,a1=10%,b1=20%.……………………………………………………2分
(Ⅰ)依题设,a1=10%,b1=20%.……………………………………………………2分
(Ⅱ) ∵an=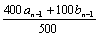 =
=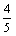 an-1+
an-1+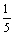 bn-1,
bn-1,
bn=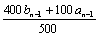 =
=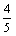 bn-1+
bn-1+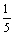 an-1.……………………………………………………4分
an-1.……………………………………………………4分
∴bn-an=(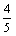 bn-1+
bn-1+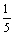 an-1)-(
an-1)-(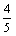 an-1+
an-1+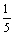 bn-1)=
bn-1)=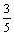 ( bn-1-an-1)(n≥2).
( bn-1-an-1)(n≥2).
可知数列{ bn-an }为首项是b1-a1=10%,公比为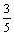 的等比数列,
的等比数列,
∴bn-an=(b1-a1)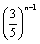 =10%
=10%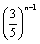 =
=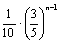 .……………………………………9分
.……………………………………9分
(Ⅲ) 由(Ⅱ) bn-an=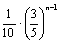 ………………………①
………………………①
又an+bn=an-1+bn-1=…=a1+b1=30%=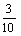 ……②…………………………………10分
……②…………………………………10分
联立①②得an=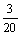 -
-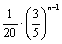 , bn=
, bn=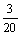 +
+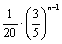 .……………………………13分
.……………………………13分
19.
(Ⅱ)h(x)=f3(x)-f2(x)=x(1+x)2,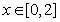
∴h ' (x)=(1+x)2+2x(1+x)=(1+x)(1+3x),
令h ' (x)=0,得x=-1或x=-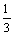 ,………………8分
,………………8分
|
x |
-2 |
(-2, -1) |
-1 |
(-1, -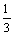 ) ) |
-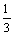 |
(-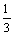 , 0) , 0) |
0 |
|
h ' (x) |
|
+ |
0 |
- |
0 |
+ |
|
|
h(x) |
-2 |
↗ |
0 |
↘ |
-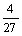 |
↗ |
0 |
 h(x)在(-2, -1),(-
h(x)在(-2, -1),(-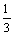 , 0)上单调递增,在(-1, -
, 0)上单调递增,在(-1, -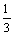 )上单调递减,过点(0, 0).
)上单调递减,过点(0, 0).
18.(Ⅰ) 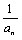 =(-1)n-
=(-1)n-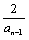 ,∴
,∴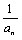 +(-1)n=(-2) [
+(-1)n=(-2) [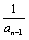 +(-1)n-1]
+(-1)n-1]
∴数列{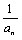 +(-1)n}是以
+(-1)n}是以 +(-1)=3为首项,公比为-2的等比数列.……………4分
+(-1)=3为首项,公比为-2的等比数列.……………4分
∴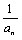 +(-1)n=3(-2) n-1,即an=
+(-1)n=3(-2) n-1,即an=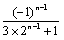 .…………………………………………6分
.…………………………………………6分
(Ⅱ) bn=(3×2 n-1+1)2=9×4 n-1+6×2 n-1+1.…………………………………………8分
∴Sn=9×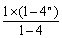 +6×
+6×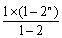 +n=3×4 n+6×2 n+n-9.………………………12分
+n=3×4 n+6×2 n+n-9.………………………12分
21.(本题满分13分)对于函数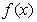 ,若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.如果函数f(x)=
,若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.如果函数f(x)=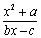 有且仅有两个不动点0和2.
有且仅有两个不动点0和2.
(Ⅰ)试求b、c满足的关系式;
(Ⅱ)若c=2时,各项不为零的数列{an}满足4Sn·f(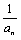 )=1,求证:
)=1,求证: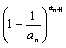 <
<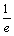 <
<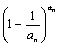 ;
;
(Ⅲ)设bn=-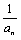 ,Tn为数列{bn}的前n项和,求证:T2009-1<ln2009<T2008.
,Tn为数列{bn}的前n项和,求证:T2009-1<ln2009<T2008.

 答
案
答
案
 ∴
∴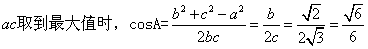 .
.
∴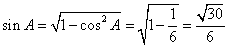
∴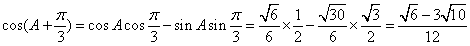 ……12分
……12分
20.(本题满分13分)现有甲、乙两个容器,分别盛有浓度为10%、20%的某种饮料各500ml.实验人员对它们进行调和试验,调和操作程序是同时从甲、乙两个容器中各取出100ml溶液,分别倒入对方容器中并充分搅拌均匀,称为第一次调和;然后又同时从第一次调和后的甲、乙两个容器中各取出100ml溶液分别倒入对方容器中并充分搅拌均匀,称为第二次调和;…依照上述操作程序反复进行调和试验,记第n-1(n∈N*)次调和后甲、乙两个容器中饮料的浓度分别为an 和bn.
(Ⅰ) 试写出a1 和b1的值;
(Ⅱ) 依据调和程序,试用n表示甲、乙两个容器中两种饮料的浓度的差bn-an;
(Ⅲ) 试求出第n-1(n∈N*)次调和后甲、乙两个容器中饮料的浓度an 、bn关于n的表达式.




湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com