
19.(本题满分13分)已知函数fn(x)=(1+x)n-1,(n∈N*,且n>1).
(Ⅰ) 设函数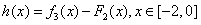 ,求
,求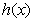 的最大值和最小值
的最大值和最小值
(Ⅱ) 若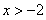 求证:fn(x)≥nx.
求证:fn(x)≥nx.













18.(本题满分12分)已知数列{an}满足a1=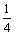 ,an=
,an=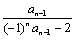 (n≥2,n∈N*).
(n≥2,n∈N*).
(Ⅰ) 证明:数列{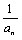 +(-1)n}是等比数列;
+(-1)n}是等比数列;
(Ⅱ) 设bn=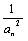 ,求数列{bn}的前n项和Sn;
,求数列{bn}的前n项和Sn;












17.(本题满分12分)在△ABC中,a、b、c分别为三个内角A、B、C的对边,锐角B满足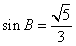 。
。
(Ⅰ) 求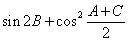 的值;
的值;
(Ⅱ) 若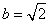 ,当ac取最大值时,求
,当ac取最大值时,求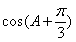 的值.
的值.













16.(本题满分12分)已知函数f(x)=2x2-2ax+b,f(-1)=-8.对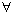 x∈R,都有f(x)≥f(-1)成立;记集合A={ x | f(x)>0},B={ x | | x-t |≤1 }.
x∈R,都有f(x)≥f(-1)成立;记集合A={ x | f(x)>0},B={ x | | x-t |≤1 }.
 (Ⅰ) 当t=1时,求( RA)∪B;
(Ⅰ) 当t=1时,求( RA)∪B;
(Ⅱ) 设命题P:A∩B≠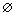 ,若┐P为真命题,求实数t的取值范围.
,若┐P为真命题,求实数t的取值范围.











15.对于函数f(x)=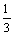 |x|3-
|x|3-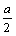 x2+(3-a)|x|+b,⑴若f(2)=7,则f(-2)=
;
x2+(3-a)|x|+b,⑴若f(2)=7,则f(-2)=
;
⑵若f(x)有六个不同的单调区间,则a的取值范围是
.

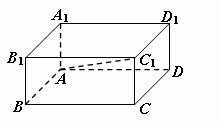
14.矩形ABCD中,对角线AC与边AB、AD所成的角分别为a、b,则cos2a+cos2b=1.如图,在长方体ABCD-A1B1C1D1中,请应用类比推理,写出一个类似的结论:

.

13.如图,已知非零向量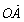 、
、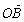 与向量
与向量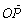 共面,且夹角分别
共面,且夹角分别
为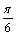 和
和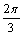 ,设
,设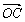 =
=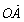 -
-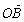 ,则向量
,则向量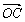 与
与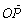 的夹角的取值
的夹角的取值
范围是
.
12.函数y=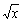 +
+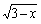 的最大值为
.
的最大值为
.
11. 已知函数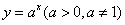 的反函数是
的反函数是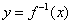 ,若
,若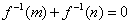 ,则m+n的最小值是_______.
,则m+n的最小值是_______.

10.定义运算: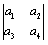 =a1a4-a2a3,则函数f(x)=
=a1a4-a2a3,则函数f(x)=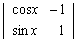 的最大值是
.
的最大值是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com