
20.解:(1) 函数
函数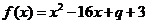 的对称轴是
的对称轴是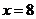
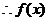 在区间
在区间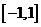 上是减函数,
上是减函数,
 函数在区间
函数在区间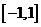 上存在零点,则必有:
上存在零点,则必有:
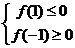 即
即
(2) ,
,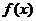 在区间
在区间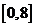 上是减函数,
上是减函数,
在区间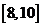 上是增函数且对称轴是
上是增函数且对称轴是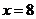
当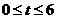 时,在区间
时,在区间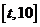 上,
上,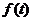 最大,
最大,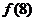 最小,
最小,
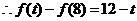 即:
即: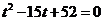 ,解得:
,解得: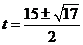 ,
,

当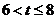 时,在区间
时,在区间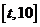 上,
上,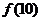 最大,
最大,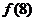 最小,
最小,
 解得:
解得:
当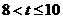 时,在区间
时,在区间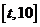 上,
上,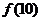 最大,
最大,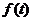 最小,
最小,
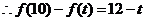 即:
即: ,解得:
,解得: 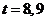
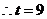
综上:存在常数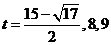 满足条件
满足条件
18.
解:(I)由函数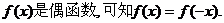
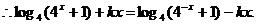 …………2分
…………2分
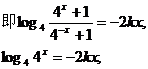
 …………4分
…………4分
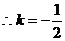 …………6分
…………6分
(II)由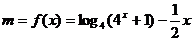 ,
,
 …………8分
…………8分
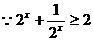 , …………10分
, …………10分
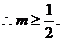
故要使方程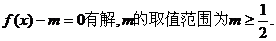 …………12分
…………12分
19 (1)  …………3’
…………3’
等号当x=2时成立,
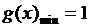 …………………………4’
…………………………4’
(2)设P(x,y)则Q(2-x,4-y)………………………………………………5’
由4-y=lg(2-x)可得:y=4-lg(2-x)………………………………8’
(3) h(x)=_______y=2x等_______, φ(x)=____y=lgx等__
17. .(1)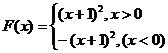
(2)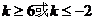
(3)能大于0
16.、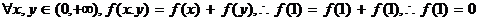 ∵0<x<1时,f(x)>0,又f(1)=f(x)+f(
∵0<x<1时,f(x)>0,又f(1)=f(x)+f( )=0,
)=0,
∴x>1时,f(x)=-
(2)f(x)在(0,+∞)上是减函数,
设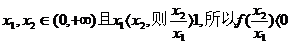 ,
,
所以
即
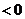
所以f(x)在(0,+∞) 上是减函数.
13. 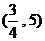 14、 ①②④
14、 ①②④
(15)解:(Ⅰ)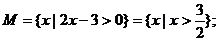
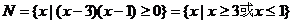
(Ⅱ)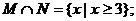
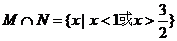 .
.
10、 .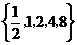 11、 .[1,+∞] 12.
11、 .[1,+∞] 12. 
6、
 7、 .[5,+∞] 8、
7、 .[5,+∞] 8、  9、已
9、已 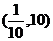
1、  2、 720 3、
2、 720 3、 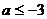 4、 (4) 5、 1
4、 (4) 5、 1
20.已知二次函数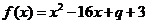
(1)
若函数在区间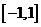 上存在零点,求实数
上存在零点,求实数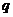 的取值范围;
的取值范围;
(2)
问:是否存在常数 ,当
,当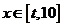 时,
时, 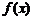 的值域为区间
的值域为区间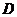 ,且
,且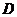 的长度为
的长度为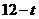 .
.
高三数学练习卷二
19. 已知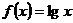
(1)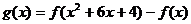 , 求
, 求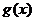 的最小值
的最小值
(2)P、Q关于点(1,2)对称,若点P在曲线C上移动时,点Q的轨迹是函数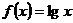 的图象,求曲线C的轨迹方程。
的图象,求曲线C的轨迹方程。
(3)在中学数学中,从特殊到一般,从具体到抽象是常见的一种思维形式。如从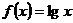 可抽象出
可抽象出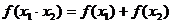 的性质,试分别写出一个具体的函数,抽象出下列相应的性质
的性质,试分别写出一个具体的函数,抽象出下列相应的性质
由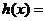 可抽象出
可抽象出
由 可抽象出
可抽象出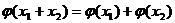
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com