
12.(学军中学2008-2009学年上学期高三期中数学试题(理))(14分)已知二次函数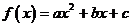 .
.
(1)若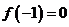 ,试判断函数
,试判断函数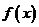 零点个数; (第11题图)
零点个数; (第11题图)
(2)是否存在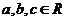 ,使
,使 同时满足以下条件①对
同时满足以下条件①对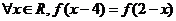 ,且
,且 ;②对
;②对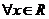 ,都有
,都有 。若存在,求出
。若存在,求出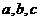 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
解:(1)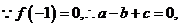
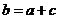
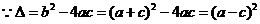 当
当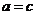 时
时 ,
,
函数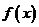 有一个零点;当
有一个零点;当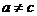 时,
时,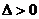 ,函数
,函数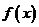 有两个零点。……6分
有两个零点。……6分
(2)假设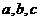 存在,由①知抛物线的对称轴为x=-1,且
存在,由①知抛物线的对称轴为x=-1,且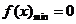
∴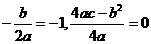
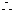
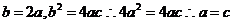
由②知对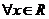 ,都有
,都有
令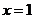 得
得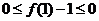
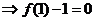
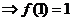
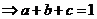
由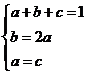 得
得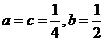 ,
,
当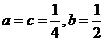 时,
时,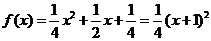 ,其顶点为(-1,0)满足条件①,又
,其顶点为(-1,0)满足条件①,又
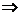 对
对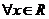 ,都有
,都有 ,满足条件②。∴存在
,满足条件②。∴存在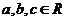 ,使
,使 同时满足条件①、②。……………………………14分
同时满足条件①、②。……………………………14分
11.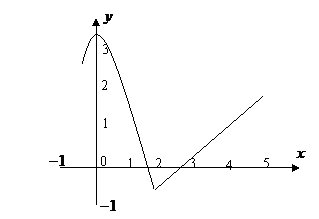 (绍兴市2008学年第一学期统考数学试题)已知函数
(绍兴市2008学年第一学期统考数学试题)已知函数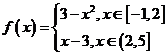 ,
,
(1)在如图给定的直角坐标系内画出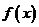 的图象;
的图象;
(2)写出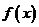 的单调递增区间.
的单调递增区间.
解析:(1)函数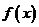 的图象如图所示:
的图象如图所示:
(2)函数的单调递增区间为
10.(2009年浙江省杭州市第一次高考科目教学质量检测数学试题(文))(本题15分)已知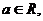 函数
函数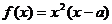 .
.
(Ⅰ)当a=3时,求f(x)的零点;
(Ⅱ)求函数y=f (x)在区间 [ 1,2 ] 上的最小值.
解:(Ⅰ) 由题意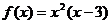 ,
,
由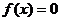 ,解得
,解得 或
或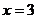 ;
--- 4分
;
--- 4分
(Ⅱ) 设此最小值为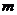 ,而
,而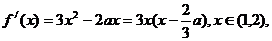
(1)当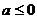 时,
时,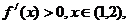
则 是区间[1,2]上的增函数, 所以
是区间[1,2]上的增函数, 所以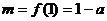 ;
--- 3分
;
--- 3分
(2)当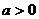 时,
时,
在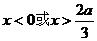 时,
时,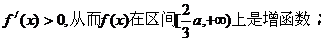
在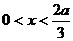 时,
时,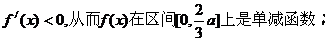 --- 3分
--- 3分
① 当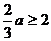 ,即
,即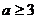 时,
时,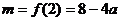 ;
;
② 当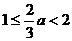 ,即
,即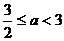 时,
时,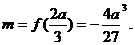
③ 当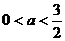 时,
时,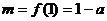 .
.
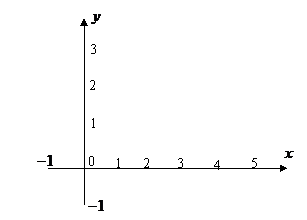 综上所述,所求函数的最小值
综上所述,所求函数的最小值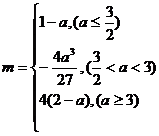 .
--- 5分
.
--- 5分
9. (2009年浙江省杭州市第一次高考科目教学质量检测数学试题(文))(本题14分)设 是定义在
是定义在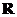 上的奇函数,且当
上的奇函数,且当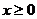 时,
时,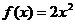 .
.
(Ⅰ) 求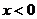 时,
时, 的表达式;
的表达式;
(Ⅱ) 令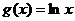 ,问是否存在
,问是否存在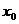 ,使得
,使得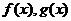 在x = x0处的切线互相平行?若存在,请求出
在x = x0处的切线互相平行?若存在,请求出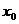 值;若不存在,请说明理由.
值;若不存在,请说明理由.
解:(Ⅰ) 当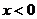 时,
时,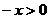 ,
,
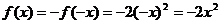 ;
--- 6分
;
--- 6分
(Ⅱ)若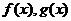 在
在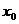 处的切线互相平行,则
处的切线互相平行,则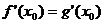 , --- 4分
, --- 4分
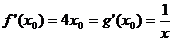 ,解得,
,解得, 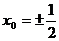
∵x > 0 , 得.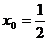 --- 4分
--- 4分
8. (2008-2009学年上学期期中高三数学试题(文))(14分)设函数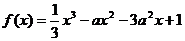 (a>0)
(a>0)
(1)求函数 的单调区间,极大值,极小值
的单调区间,极大值,极小值
(2)若 时,恒有
时,恒有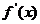 >
>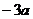 ,求实数a的取值范围
,求实数a的取值范围
解:(1)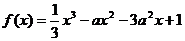
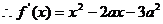 …………………………2分
…………………………2分
令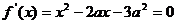
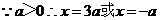
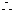
|
x |
(- ,-a) ,-a) |
-a |
(-a,3a) |
3a |
(3a,+ ) ) |
y |
+ |
0 |
- |
0 |
+ |
|
y |
增 |
极大值 |
减 |
极小值 |
增 |
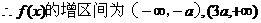
减区间为 (-a,3a)
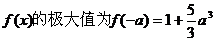
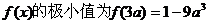 …………………..8分
…………………..8分
(2)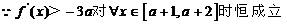
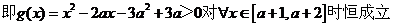
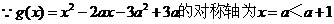
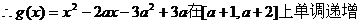 ……………………11分
……………………11分
只需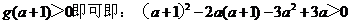
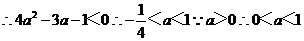 …………………………………..14分
…………………………………..14分
7.(2008学年第一学期十校高三期末联考数学试题(文))(15分)设函数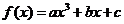
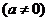 为奇函数,其图象在点
为奇函数,其图象在点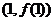 处的切线与直线
处的切线与直线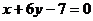 垂直,且在x=-1处取得极值.
垂直,且在x=-1处取得极值.
(Ⅰ)求a,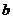 ,
,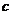 的值;
的值;
(Ⅱ)求函数 在
在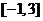 上的最大值和最小值。
上的最大值和最小值。
解: (Ⅰ)∵ 为奇函数,∴
为奇函数,∴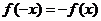
即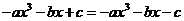
∴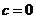 ----------------------1分
----------------------1分
∵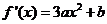 的最小值为
的最小值为 ,
,
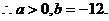 -----------3分
-----------3分
又直线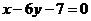 的斜率为
的斜率为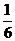
因此,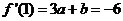 ------------5分
------------5分
∴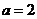 ,
,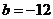 ,
,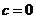 .
-------------7分
.
-------------7分
(Ⅱ)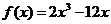 .
.
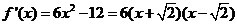 ,列表如下:
,列表如下:
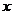 |
 |
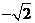 |
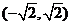 |
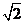 |
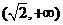 |
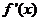 |
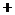 |
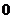 |
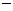 |
 |
 |
 |
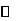 |
极大 |
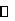 |
极小 |
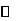 |
-----------11分
∵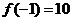 ,
,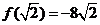 ,
,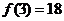
∴ 在
在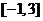 上的最大值是
上的最大值是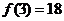 ,最小值是
,最小值是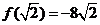 . ---------15分
. ---------15分
6.(2008学年第一学期十校高三期末联考数学试题(理))(本小题满分14分) 已知函数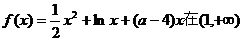 上是增函数.
上是增函数.
(I)求实数a的取值范围;
(II)在(I)的结论下,设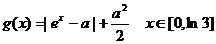 ,求函数
,求函数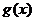 的最小值.
的最小值.
解:(I)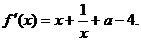 …………………………………………… 2分
…………………………………………… 2分
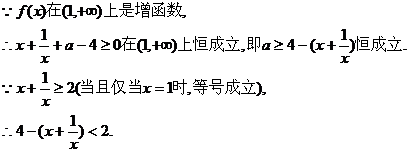
所以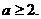 ……………………………………………………………………7分
……………………………………………………………………7分
(II)设
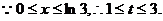 ……8分
……8分
当 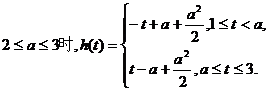 …………………………10分
…………………………10分
 …………………………………………11分
…………………………………………11分
当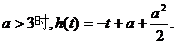
 ……………………………………13分
……………………………………13分
所以,当
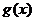 的最小值为
的最小值为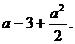 ……………………………………………… 14分
……………………………………………… 14分
5.(宁波市2008学年度第一学期高三期末数(理))(本题14分)已知函数 和点
和点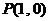 ,过点
,过点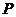 作曲线
作曲线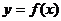 的两条切线
的两条切线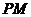 、
、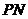 ,切点分别为
,切点分别为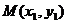 、
、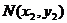 .
.
(1)求证: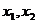 为关于
为关于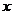 的方程
的方程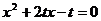 的两根;
的两根;
(2)设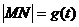 ,求函数
,求函数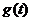 的表达式;
的表达式;
(3)在(2)的条件下,若在区间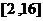 内总存在
内总存在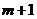 个实数
个实数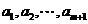 (可以相同),使得不等式
(可以相同),使得不等式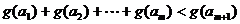 成立,求
成立,求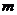 的最大值.
的最大值.
解:(1)由题意可知: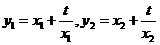
∵ 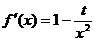 , ……2分
, ……2分
∴切线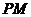 的方程为:
的方程为: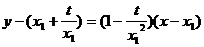 ,
,
又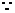 切线
切线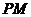 过点
过点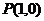 ,
,  有
有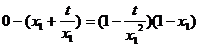 ,
,
即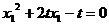 , ①
, ①
同理,由切线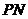 也过点
也过点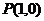 ,得
,得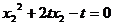 .②
.②
由①、②,可得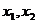 是方程
是方程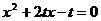 ( * )的两根……5分
( * )的两根……5分
(2)由( * )知. 
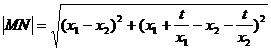
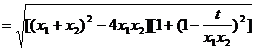
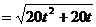 ,
,
∴  .……………………9分
.……………………9分
(3)易知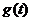 在区间
在区间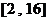 上为增函数,
上为增函数,
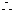
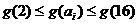
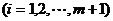 ,
,
则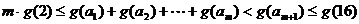 .…11分
.…11分
即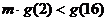 ,即
,即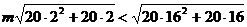 ,
,
所以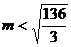 ,由于
,由于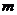 为正整数,所以
为正整数,所以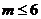 .
.
又当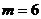 时,存在
时,存在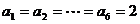 ,
,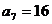 满足条件,所以
满足条件,所以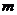 的最大值为
的最大值为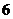 .
……………14分
.
……………14分
4.(学军中学2008-2009学年上学期高三期中数学试题(理))( 14分)设函数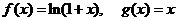
(1) 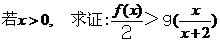
(2)是否存在实数m,使函数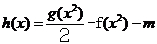 恰有四个不同的零点?若存在求出的m范围;若不存在,说明理由。
恰有四个不同的零点?若存在求出的m范围;若不存在,说明理由。
解:(1)证明:
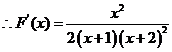
易知F(X)在[0,+∞)为增函数,所以F(X)> F(0)=0,即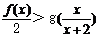 ……………..6分
……………..6分
(2) 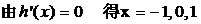 ,再由
,再由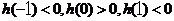
易得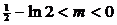 时, 函数
时, 函数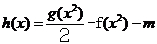 恰有四个不同的零点
恰有四个不同的零点
…………………… 14分
3.(宁波市2008学年度第一学期高三期末数(文))(本题满分14分)已知函数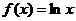 ,
,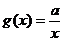 ,设
,设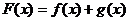 .
.
(Ⅰ)当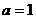 时,求函数
时,求函数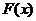 的单调区间;
的单调区间;
(Ⅱ)若以函数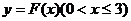 图象上任意一点
图象上任意一点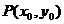 为切点的切线斜率
为切点的切线斜率
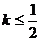 恒成立,求实数
恒成立,求实数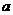 的最小值.
的最小值.
解:(Ⅰ)由已知可得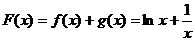 ,函数的定义域为
,函数的定义域为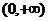
则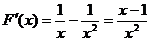
由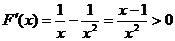 可得
可得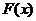 在区间
在区间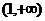 上单调递增,
上单调递增,
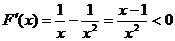 得
得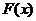 在
在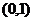 上单调递减
……6分
上单调递减
……6分
(Ⅱ)由题意可知 对任意
对任意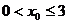 恒成立
恒成立
即有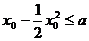 对任意
对任意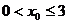 恒成立,即
恒成立,即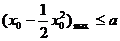
令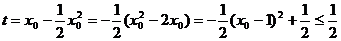
则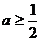 ,即实数
,即实数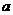 的最小值为
的最小值为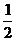 ; ……14分
; ……14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com