9．若定义在R上的函数f(x)满足f(+x)＝－f(x)，且f(－x)＝f(x)，则f(x)可以是(　)

A．f(x)＝2sinx　 　　　　　　　 B．f(x)＝2sin3x

C．f(x)＝2cosx　 　　　　　　　 D．f(x)＝2cos3x

解析：∵f(－x)＝f(x)，∴f(x)为偶函数，∴排除A、B.

又∵f(+x)＝－f(x)，∴f(x)是周期为π的函数，

∴选D.

答案：D

8．(2009·江西高考)若函数f(x)＝(1+tanx)cosx,0≤x<，则f(x)的最大值为

(　)

A．1　 　　　　　　　　　　　　　　　 B．2

C.+1　 　　　　　　　　　　　　　 D.+2

解析：f(x)＝(1+·)cosx＝cosx+sinx

＝2(cosx+sinx)＝2sin(x+)．

∵0≤x<，∴≤x+≤.

∴≤sin(x+)≤1.∴1≤f(x)≤2.

答案：B

7．已知函数y＝sin(ωx+φ)(ω>0,0<φ≤)，且此函数的图象如图1所示，由点P(ω，φ)的坐标是

(　)

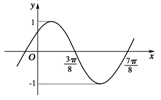
图1

A．(2，)　　　　　　　　　　　 B．(2，)

C．(4，)　　　　　　　　　　　 D．(4，)

解析：由图象可得函数的周期T＝2×(－)＝π＝，得ω＝2，将(，0)代入y＝sin(2x+φ)可得sin(+φ)＝0，由0<φ≤可得φ＝，

∴点(ω，φ)的坐标是(2，)，故选B.

答案：B

6．若α∈[π，π]，则+的值为

(　)

A．2cos　 　　　　　　　　　　　　 B．－2cos

C．2sin　 　　 　　　　　　　　　　 D．－2sin

解析：原式＝+

＝|sin+cos|+|sin－cos|.

∵α∈[，]，∴∈[，]，

当∈[，]时，sin≤cos≤0，

原式＝－(sin+cos)－(sin－cos)

＝－2sin，

当∈[，]时，sin<0，cos≥0.

且|sin|≥|cos|，

∴原式＝－(sin+cos)－(sin－cos)

＝－2sin.

综上，原式＝－2sin.

答案：D

5．将函数f(x)的图象沿x轴向右平移个单位，再将横坐标伸长为原来的2倍(纵坐标不变)，得到的图象所对应的函数为y＝cosx，则f(x)为

(　)

A．y＝cos(2x+)　 　　　　　　 B．y＝cos(2x－)

C．y＝cos(2x+π)　 　　　　　 D．y＝cos(2x－π)

解析：y＝cosxy＝cos2x

y＝cos2(x+)．

答案：C

4．已知2sin²α－sinαcosα+5cos²α＝3，则tanα的值是

(　)

A．1　 　　　　　　　　　　　　　　　 B．－2

C．1或－2　 　　　　　　　　　　　 D．－1或2

解析：由2sin²α－sinαcosα+5cos²α＝3，得

sin²α+sinαcosα－2cos²α＝0，

即tan²α+tanα－2＝0，

解之得tanα＝1或tanα＝－2.

答案：C

3．已知sinαcosα＝，且<α<，则cosα－sinα的值是

(　)

A.　 　　　　　　　　　　　　　　　　 B．－

C．－　 　　　　　　　　　　　　　　 D．±

解析：∵α∈(，)，

∴sinα>cosα，即cosα－sinα<0，

∵(cosα－sinα)²＝1－2sinαcosα＝，

∴cosα－sinα＝－.

答案：B

2．若△ABC的内角满足sinA+cosA>0，tanA－sinA<0，则角A的取值范围是(　)

A．(0，)　 　　　　　　　　　　　 B．(，)

C．(，)　 　　　　　　　　　　　 D．(，π)

解析：由tanA<sinA可知A为钝角，又sinA+cosA>0，结合单位圆可知A∈(，)．

答案：C

1．角α的终边经过点P(x，－)(x≠0)，且cosα＝x，则sinα等于

(　)

A.x　　　　　 B.

C.x　 　　　　　　　　　　　　　　 D．－

解析：r＝，

∵cosα＝x，∴＝，

∴＝，

∴sinα＝＝－＝－.

答案：D

13.中国共产党领导的多党合作和政治协商制度，是中国特色社会主义民主政治的一大特色。通过政治协商，可以妥善化解人民内部的各种矛盾，使人民内部的局部利益、个别利益与整体利益、根本利益相互协调。中国共产党领导的多党合作和政治协商制度在构建社会主义和谐社会中占有重要的地位，发挥着不可替代的作用。

(1)简述中国共产党领导的多党合作和政治协商制度的优越性。

(2)请从我国政党制度的角度，谈谈如何构建社会主义和谐社会？

解析：本题主要考查我国政党制度的有关知识。第(1)问只要对教材知识识记即可；第(2)问可从中国共产党、中国共产党与各民主党派的关系、参政党的角度来回答。

答案：(1)坚持和完善中国共产党领导的多党合作制度，有利于发展社会主义民主政治；有利于发展社会主义经济和文化；有利于构建社会主义和谐社会；有利于推进祖国和平统一大业。

(2)①中国共产党是多党合作的领导力量。构建和谐社会必须坚持、加强和改善中国共产党的领导，提高党的领导能力和执政水平。②构建和谐社会必须正确处理好中国共产党与各民主党派的关系。中国共产党要发扬民主，广开言路、广求良策；各民主党派要从国家和民族的整体利益出发，履行政治协商、民主监督和参政议政职能；中国共产党和各民主党派要互相尊重、平等相待、民主协商、真诚合作、互相监督。③构建和谐社会必须加强参政党建设，提高其参政议政能力。