
21、(本小题满分15分)
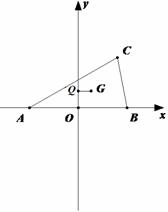
设Q、G分别为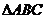 的外心和重心,已知
的外心和重心,已知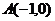 ,
,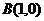 ,
,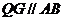 。
。
 (1)求点
(1)求点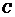 的轨迹
的轨迹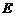 。
。
(2)轨迹E与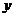 轴两个交点分别为
轴两个交点分别为 ,
,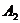 (
( 位于
位于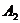 下方)。动点M、N均在轨迹E上,且满足
下方)。动点M、N均在轨迹E上,且满足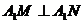 ,试问直线
,试问直线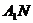 和
和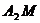 交点P是否恒在某条定直线
交点P是否恒在某条定直线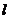 上?若是,试求出
上?若是,试求出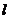 的方程;若不是,请说明理由。
的方程;若不是,请说明理由。
20、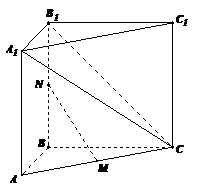 (本小题满分14分)
(本小题满分14分)
如图,在直三棱柱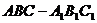 中,
中,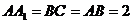 ,
,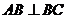 。M、N分别是AC和BB1的中点。
。M、N分别是AC和BB1的中点。
(1)求二面角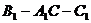 的大小。
的大小。
(2)证明:在AB上存在一个点Q,使得平面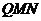 ⊥平面
⊥平面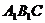 ,并求出
,并求出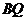 的长度。
的长度。
19、(本小题满分14分)
甲乙两队参加某知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分。假设甲队中每人答对的概率均为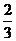 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为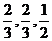 且各人回答正确与否相互之间没有影响.用ξ表示乙队的总得分.
且各人回答正确与否相互之间没有影响.用ξ表示乙队的总得分.
(Ⅰ)求随机变量ξ的分布列和数学期望;
(Ⅱ)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求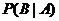 。
。
18、(本小题满分14分)
已知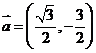 ,
,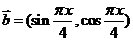 ,
,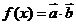 。
。
(1)求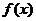 的单调递减区间。
的单调递减区间。
(2)若函数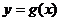 与
与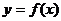 关于直线
关于直线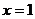 对称,求当
对称,求当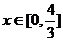 时,
时,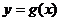 的最大值。
的最大值。
17、在三棱柱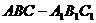 中,各棱长都等于2a,下底面
中,各棱长都等于2a,下底面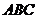 在水平面上保持不动,在侧棱与底面所成的角保持为60°的情况下,上底面
在水平面上保持不动,在侧棱与底面所成的角保持为60°的情况下,上底面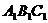 还是可以移动的,则△
还是可以移动的,则△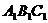 在下底面
在下底面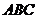 所在平面上的竖直投影所扫过的区域的面积为 ▲ 。
所在平面上的竖直投影所扫过的区域的面积为 ▲ 。
16、甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人至少参加一天且每天都安排一人,并要求甲必须安排在另外两位前面。不同的安排方法共有 ▲ 种。
15、观察下列等式: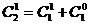
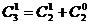
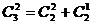
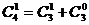
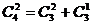
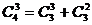 ………
………
由以上等式推测到一个一般性的结论:对任意的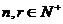 (
(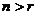 ),
),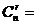 ▲ 。
▲ 。
14、一个水池容积为100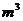 ,装有甲、乙、丙三个水管,甲乙为进水管,丙为出水管。单开甲管2小时可将空水池注满,单开乙管3小时可将空水池注满,单开丙管6小时将满池水放空。三管齐开,1.8小时后水池中的水量为 ▲
,装有甲、乙、丙三个水管,甲乙为进水管,丙为出水管。单开甲管2小时可将空水池注满,单开乙管3小时可将空水池注满,单开丙管6小时将满池水放空。三管齐开,1.8小时后水池中的水量为 ▲ 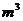 。
。
13、若实数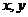 满足不等式组
满足不等式组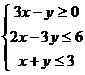 ,则
,则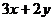 的最大值是 ▲ 。
的最大值是 ▲ 。
12、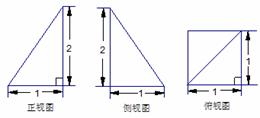 已知四棱锥P-ABCD的三视图如图所示,则该四棱锥的表面积为 ▲ 。
已知四棱锥P-ABCD的三视图如图所示,则该四棱锥的表面积为 ▲ 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com