
(一)选择题:
1、(06全国Ⅱ)函数y=lnx-1(x>0)的反函数为( )
A、y=ex+1(x∈R) B、y=ex-1(x∈R)
C、y=ex+1(x>1) D、y=ex-1(x>1)
2、(05全国Ⅲ)设 ,则( )
,则( )
A、-2< <-1 B、-3<
<-1 B、-3< <-2 C、-1<
<-2 C、-1< <0 D、0<
<0 D、0< <1
<1
3、(04天津11)函数 (
(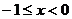 )的反函数是
)的反函数是
A.  B.
B.

C.  D.
D.

4、(04湖北)若函数 、三、四象限,则一定有( )
、三、四象限,则一定有( )
A.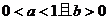 B.
B.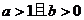
C.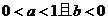 D.
D.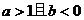
例1、(07江苏)设函数 定义在实数集上,它的图像关于直线
定义在实数集上,它的图像关于直线 对称,且当
对称,且当 时,
时, ,则有( )
,则有( )
A. B.
B.
C. D.
D.
例2、(07上海春)若 为方程
为方程 的两个实数解,则
的两个实数解,则 ;
;
例3、(05全国Ⅱ)设函数 ,求使
,求使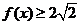 的
的 取值范围.
取值范围.
例4、(05江西10)已知实数a, b满足等式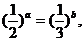 下列五个关系式
下列五个关系式
①0<b<a ②a<b<0 ③0<a<b ④b<a<0 ⑤a=b
其中不可能成立的关系式有( )
A.1个 B.2个 C.3个 D.4个
例5、(06湖北21)设 是函数
是函数 的一个极值点。(Ⅰ)、求
的一个极值点。(Ⅰ)、求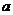 与
与 的关系式(用
的关系式(用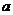 表示
表示 ),并求
),并求 的单调区间;(Ⅱ)、设
的单调区间;(Ⅱ)、设 ,
,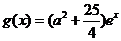 。若存在
。若存在 使得
使得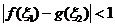 成立,求
成立,求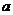 的取值范围。 点评:本小题主要考查函数、不等式和导数的应用等知识,考查综合运用数学知识解决问题的能力。
的取值范围。 点评:本小题主要考查函数、不等式和导数的应用等知识,考查综合运用数学知识解决问题的能力。
解:(Ⅰ)f `(x)=-[x2+(a-2)x+b-a ]e3-x,
由f `(3)=0,得 -[32+(a-2)3+b-a ]e3-3=0,即得b=-3-2a,
则 f `(x)=[x2+(a-2)x-3-2a-a ]e3-x
=-[x2+(a-2)x-3-3a ]e3-x=-(x-3)(x+a+1)e3-x.
令f `(x)=0,得x1=3或x2=-a-1,由于x=3是极值点,
所以x+a+1≠0,那么a≠-4.
当a<-4时,x2>3=x1,则
在区间(-∞,3)上,f `(x)<0, f (x)为减函数;
在区间(3,―a―1)上,f `(x)>0,f (x)为增函数;
在区间(―a―1,+∞)上,f `(x)<0,f (x)为减函数。
当a>-4时,x2<3=x1,则
在区间(-∞,―a―1)上,f `(x)<0, f (x)为减函数;
在区间(―a―1,3)上,f `(x)>0,f (x)为增函数;
在区间(3,+∞)上,f `(x)<0,f (x)为减函数。
(Ⅱ)由(Ⅰ)知,当a>0时,f (x)在区间(0,3)上的单调递增,在区间(3,4)上单调递减,那么f (x)在区间[0,4]上的值域是[min(f (0),f (4) ),f (3)],
而f (0)=-(2a+3)e3<0,f (4)=(2a+13)e-1>0,f (3)=a+6,
那么f (x)在区间[0,4]上的值域是[-(2a+3)e3,a+6].
又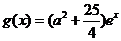 在区间[0,4]上是增函数,
在区间[0,4]上是增函数,
且它在区间[0,4]上的值域是[a2+ ,(a2+
,(a2+ )e4],
)e4],
由于(a2+ )-(a+6)=a2-a+
)-(a+6)=a2-a+ =(
=( )2≥0,所以只须仅须
)2≥0,所以只须仅须
(a2+ )-(a+6)<1且a>0,解得0<a<
)-(a+6)<1且a>0,解得0<a< .
.
故a的取值范围是(0, )。
)。
例3 函数 的定义域是全体实数,则实数m的取值范围是( ).A.
的定义域是全体实数,则实数m的取值范围是( ).A. B.
B. C.
C. D.
D.
解析:要使函数 的定义域是全体实数,可转化为
的定义域是全体实数,可转化为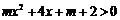 对一切实数都成立,即
对一切实数都成立,即 且
且 .
.
解得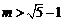 . 故选(B)
. 故选(B)
幂函数中的三类讨论题
所谓分类讨论,实质上是“化整为零,各个击破,再积零为整”的策略. 分类讨论时应注重理解和掌握分类的原则、方法与技巧,做到确定对象的全体,明确分类的标准,不重、不漏的分类讨论.在幂函数中,分类讨论的思想得到了重要的体现,可根据幂函数的图象和性质,依据幂函数的单调性分类讨论,使得结果得以实现.
类型一:求参数的取值范围
例1 已知函数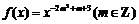 为偶函数,且
为偶函数,且 ,求m的值,并确定
,求m的值,并确定 的解析式.
的解析式.
分析:函数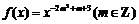 为偶函数,已限定了
为偶函数,已限定了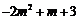 必为偶数,且
必为偶数,且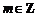 ,
, ,只要根据条件分类讨论便可求得m的值,从而确定
,只要根据条件分类讨论便可求得m的值,从而确定 的解析式.
的解析式.
解:∵ 是偶函数,∴
是偶函数,∴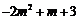 应为偶数.
应为偶数.
又∵ ,即
,即 ,整理,得
,整理,得 ,∴
,∴ ,∴
,∴ .
.
又∵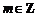 ,∴
,∴ 或1.
或1.
当m=0时, 为奇数(舍去);当
为奇数(舍去);当 时,
时, 为偶数.
为偶数.
故m的值为1, .
.
评注:利用分类讨论思想解题时,要充分挖掘已知条件中的每一个信息,做到不重不漏,才可为正确解题奠定坚实的基础.
类型二:求解存在性问题
例2 已知函数 ,设函数
,设函数 ,问是否存在实数
,问是否存在实数 ,使得
,使得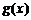 在区间
在区间 是减函数,且在区间
是减函数,且在区间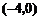 上是增函数?若存在,请求出来;若不存在,请说明理由.
上是增函数?若存在,请求出来;若不存在,请说明理由.
分析:判断函数的单调性时,可以利用定义,也可结合函数的图象与性质进行判断,但要注意问题中符号的确定,要依赖于自变量的取值区间.
解:∵ ,则
,则 .
.
假设存在实数 ,使得
,使得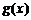 满足题设条件,
满足题设条件,
设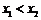 ,则
,则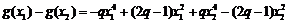
 .
.
若 ,易知
,易知 ,
, ,要使
,要使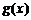 在
在 上是减函数,则应有
上是减函数,则应有 恒成立.
恒成立.
∵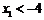 ,
, ,∴
,∴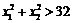 .而
.而 ,
,
∴ ..
..
从而要使 恒成立,则有
恒成立,则有 ,即
,即 .
.
若 ,易知
,易知 ,要使
,要使 在
在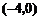 上是增函数,则应有
上是增函数,则应有 恒成立.
恒成立.
∵ ,
,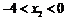 ,
,
∴ ,而
,而 ,∴
,∴ .
.
要使 恒成立,则必有
恒成立,则必有 ,即
,即 .
.
综上可知,存在实数 ,使得
,使得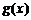 在
在 上是减函数,且在
上是减函数,且在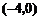 上是增函数.
上是增函数.
评注:本题是一道综合性较强的题目,是幂函数性质的综合应用.判断函数的单调性时,可从定义入手,也可根据函数图象和性质进行判断,但对分析问题和解决问题的能力要求较高,这在平时要注意有针对性的训练.
类型三:类比幂函数性质,讨论函数值的变化情况
例3 讨论函数 在
在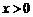 时随着x的增大其函数值的变化情况.
时随着x的增大其函数值的变化情况.
分析:首先应判定函数是否为常数函数,再看幂指数,并参照幂函数的性质讨论.
解:(1)当 ,即
,即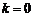 或
或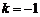 时,
时, 为常函数;
为常函数;
(2)当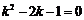 时,
时, 或
或 ,此时函数为常函数;
,此时函数为常函数;
(3) 即
即 时,函数为减函数,函数值随x的增大而减小;
时,函数为减函数,函数值随x的增大而减小;
(4)当 即
即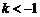 或
或 时,函数为增函数,函数值随x的增大而增大;
时,函数为增函数,函数值随x的增大而增大;
(5)当 即
即 时,函数为增函数,函数值随x的增大而增大;
时,函数为增函数,函数值随x的增大而增大;
(6)当 ,即
,即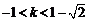 时,函数为减函数,函数值随x的增大而减小.
时,函数为减函数,函数值随x的增大而减小.
评注:含参数系数问题,可以说是解题中的一个致命杀手,是导致错误的一个重要因素.这应引起我们的高度警觉.
幂函数习题
幂函数这一知识点,表面上看内容少而且容易,实质上则不然.它蕴涵了数形结合、分类讨论、转化等数学思想,是培养同学们数学思维能力的良好载体.下面通过一题多变的方法探究幂函数性质的应用.
例1 若 ,试求实数m的取值范围.
,试求实数m的取值范围.
错解(数形结合):由图1可知
解得  ,且
,且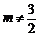 .
.
剖析:函数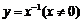 虽然在区间
虽然在区间 和
和 上分别具有单调性,但在区间
上分别具有单调性,但在区间 上不具有单调性,因而运用单调性解答是错误的.
上不具有单调性,因而运用单调性解答是错误的.
正解(分类讨论):
 (1)
(1)
解得 ;
;
(2) 此时无解;
此时无解;
(3) , 解得
, 解得 .
.
综上可得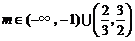 .
.
现在把例1中的指数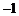 换成3看看结果如何.
换成3看看结果如何.
例2 若 ,试求实数m的取值范围.
,试求实数m的取值范围.
错解(分类讨论):由图2知,
(1) 1, 解得
1, 解得 ;
;
 (2)
(2)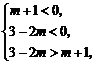 此时无解;
此时无解;
(3) , 解得
, 解得  .
.
综上可得  .
.
剖析:很明显,此解法机械地模仿例1的正确解法,而忽视了函数间定义域的不同.由此,使我们感受到了幂函数的定义域在解题中的重要作用.
正解(利用单调性):由于函数 在
在 上单调递增,所以
上单调递增,所以 ,解得
,解得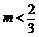 .
.
例2正确解法深化了对幂函数单调性的理解,激活了同学们的思维.下面再对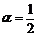 和
和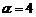 两个问题与解法进行探究.
两个问题与解法进行探究.
例3若 ,试求实数m的取值范围.
,试求实数m的取值范围.
 解:由图3,
解:由图3,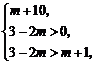 ,解得
,解得 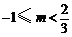 .
.
例4 若 ,试求实数m的取值范围.
,试求实数m的取值范围.
解析:作出幂函数 的图象如图4.由图象知此函数在
的图象如图4.由图象知此函数在 上不具有单调性,若分类讨论步骤较繁,把问题转化到一个单调区间上是关键.考虑
上不具有单调性,若分类讨论步骤较繁,把问题转化到一个单调区间上是关键.考虑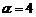 时,
时, .于是有
.于是有 ,即
,即 .
.
又∵幂函数 在
在 上单调递增,
上单调递增,
∴ , 解得
, 解得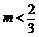 ,或m>4.
,或m>4.
上述解法意识到幂函数 在第一象限的递增性,于是巧妙运用转化思想解题,从而避免了分类讨论,使同学们的思维又一次得到深化与发展.
在第一象限的递增性,于是巧妙运用转化思想解题,从而避免了分类讨论,使同学们的思维又一次得到深化与发展.
解题点悟:通过以上探究,我们对幂函数的定义域、单调性、奇偶性及图象又有了较深刻的认识,同时对于形如 (
( 是常数)型的不等式的解法有了以下体会:
是常数)型的不等式的解法有了以下体会:
(1)当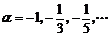 ,解法同例1
,解法同例1
(2)当 ,解法同例2
,解法同例2
(3)当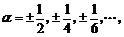 ,解法同例3
,解法同例3
(4)当 ,解法同例4.
,解法同例4.
编者点评:本文通过对一典型例题的多种变换,使我们对幂函数的性质及图象都有了较深刻的认识,其中例4解题过程中虽涉及了含绝对值不等式的解法,超出了我们的所学范围,但它其中蕴含的这种“转化”的思想,一方面拓宽了我们的解题思路,同时也体现了对知识的灵活应用能力,当然此题还可用分类讨论的方法解决,同学们不妨一试.
例2 已知点 在幂函数
在幂函数 的图象上,点
的图象上,点 ,在幂函数
,在幂函数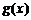 的图象上.
的图象上.
问当x为何值时有:(1) ;(2)
;(2)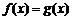 ;(3)
;(3)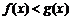 .
.
分析:由幂函数的定义,先求出 与
与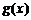 的解析式,再利用图象判断即可.
的解析式,再利用图象判断即可.
解:设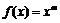 ,则由题意,得
,则由题意,得 ,
,
∴ ,即
,即 .再令
.再令 ,则由题意,得
,则由题意,得 ,
,
∴ ,即
,即 .在同一坐标系中作出
.在同一坐标系中作出
 与
与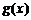 的图象,如图2所示.由图象可知:
的图象,如图2所示.由图象可知:
(1)当 或
或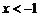 时,
时, ;
;
(2)当 时,
时,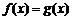 ;
;
(3)当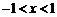 且
且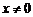 时,
时,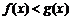 .
.
小结:数形结合在讨论不等式时有着重要的应用,注意本题中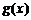 的隐含条件
的隐含条件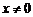 .
.
例1 已知函数
 的图象与两坐标轴都无公共点,且其图象关于y轴对称,求n的值,并画出函数的图象.
的图象与两坐标轴都无公共点,且其图象关于y轴对称,求n的值,并画出函数的图象.
解:因为图象与y轴无公共点,故 ,又图象关于y轴对称,则
,又图象关于y轴对称,则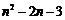 为偶数,由
为偶数,由 ,得
,得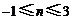 ,又因为
,又因为 ,所以
,所以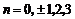 .
.
当 时,
时, 不是偶数;
不是偶数;
当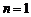 时,
时, 为偶数;
为偶数;
当 时,
时,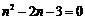 为偶数;
为偶数;
当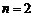 时,
时, 不是偶数;
不是偶数;
当 时,
时,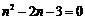 为偶数;
为偶数;
所以n为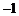 ,1或3.
,1或3.
 此时,幂函数的解析为
此时,幂函数的解析为 或
或 ,其图象如图1所示.
,其图象如图1所示.
20.(14分)利用幂函数图象,画出下列函数的图象(写清步骤).
(1) .
.
19.(14分)由于对某种商品开始收税,使其定价比原定价上涨x成(即上涨率为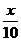 ),涨价后,商品卖出个数减少bx成,税率是新定价的a成,这里a,b均为正常数,且a<10,设售货款扣除税款后,剩余y元,要使y最大,求x的值.
),涨价后,商品卖出个数减少bx成,税率是新定价的a成,这里a,b均为正常数,且a<10,设售货款扣除税款后,剩余y元,要使y最大,求x的值.
18.(12分)下面六个幂函数的图象如图所示,试建立函数与图象之间的对应关系.


(A) (B) (C) (D) (E) (F)
17.(12分)求证:函数 在R上为奇函数且为增函数.
在R上为奇函数且为增函数.
16.(12分)已知幂函数 轴对称,试确定
轴对称,试确定 的解析式.
的解析式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com