
15. 或
或 }
} 
9. 10.
10.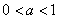 11.1 12.
11.1 12.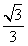 13.
13. 14.
14.
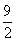
21.(本小题满分13分)
 如图,已知圆
如图,已知圆 的方程为
的方程为 ,椭圆
,椭圆 的方程为
的方程为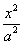

 的离心率为
的离心率为 ,如果
,如果 与
与 相交于
相交于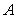 、
、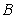 两点,
两点,
且线段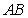 恰为圆
恰为圆 的直径,求直线
的直径,求直线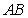 的方程和椭圆
的方程和椭圆 的方程。
的方程。
1-5 CDCDC 6-8 BBA
20.(本小题满分13分)
已知函数
(1)当 时,讨论
时,讨论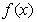 在定义域上的单调性;
在定义域上的单调性;
(2)若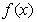 在区间
在区间 上的最小值是
上的最小值是 ,求实数
,求实数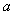 的值。
的值。
19.(本小题满分13分)
已知数列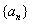 中,
中, ,且当
,且当 时,函数
时,函数
 取得极值。
取得极值。
(1)求证:数列 是等比数列;
是等比数列;
(2)当 时,求数列
时,求数列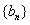 的前
的前 项和
项和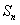 。
。
18.(本小题满分12分)
某租凭公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需要维护费200元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租凭公司的月收益最大?最大月收益是多少元?
17.(本小题满分12分)
 如图,四棱锥
如图,四棱锥 的底面是正方形,
的底面是正方形, 底面
底面 ,
,
点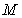 在棱PD上,且
在棱PD上,且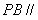 平面
平面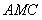 。
。
(1)试确定点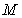 的位置;
的位置;
(2)若点 是
是 的中点,求证:
的中点,求证: 平面
平面
16.(本小题满分12分)
已知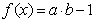 ,其中向量
,其中向量
(1)求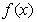 的最小正周期;
的最小正周期;
(2)在 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为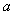 、
、 、
、 ,
, ,求边长
,求边长 的值。
的值。
15.定义在R上的偶函数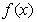 满足条件:①对任意正实数
满足条件:①对任意正实数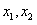 ,且
,且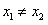 ,都有
,都有 ;②
;② ,则:
,则:
(1)不等式 的解集是______________________;
的解集是______________________;
(2)若 时,
时,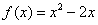 ,则
,则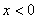 时,
时, ___________。
___________。
14.若直线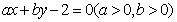 平面圆
平面圆 ,则:
,则:
(1)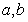 满足的条件是______________;
满足的条件是______________;
(2) 的最小值是___________。
的最小值是___________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com