
17、解:(1)因为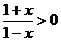 ,所以
,所以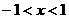 ,所以所求函数的定义域为(-1,1)(3分).
,所以所求函数的定义域为(-1,1)(3分).
(2) 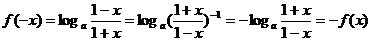 ,所以
,所以 为奇函数( 6分).
为奇函数( 6分).
(3)设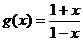 ,任取
,任取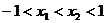 ,则
,则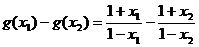
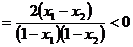 ,所以
,所以 在 (-1,1)为增函数(10分).所以当
在 (-1,1)为增函数(10分).所以当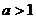 时,
时, 为增函数;当
为增函数;当 时,
时,  为递减函数(12分).
为递减函数(12分).
16、解:由A={1,2,x2-5x+9}={1,2,3},知x2-5x+9=3,解得x=2或x=3,
又2 ∈B,则x2+ax+a=2,当x=2时,a= ,当x=3时,a=
,当x=3时,a=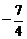 .
.
故a= 或
或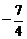
21、(满分13分)
函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性等,请选择适当的探究顺序,研究函数f(x)=
+的性质,并在此基础上,作出其在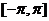 的草图.
的草图.
|
一:选择题(本大题8小题,每题5分,共40分)
二、填空题(本大题7小题,每题5分,共35分)
20、(满分13分)
某租赁公司拥有汽车100辆,当每辆汽车的月租金为3000元时,可全部租出。当每辆车的月租金每增加50元时,未租出的车辆会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元。
(1) 当每辆车的月租金定为3600元时,能租出多少辆车?
(2) 当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
19、(满分13分)已知定义在区间上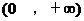 的函数f(x)满足
的函数f(x)满足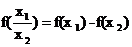 且当x>1时f(x)<0
且当x>1时f(x)<0
(1)求f(1)的值
(2)判断f(x)的单调性
(3)若f(3)=-1解不等式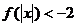
18、(满分12分)
已知二次函数 。
。
⑴ 若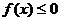 的解集为
的解集为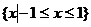 ,求实数
,求实数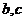 的值;
的值;
⑵ 若 满足
满足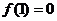 ,且关于
,且关于 的方程
的方程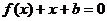 的两个实根分别在区间
的两个实根分别在区间
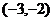 和
和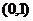 内,求实数
内,求实数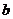 的取值范围。
的取值范围。
17、(满分12分)
已知
 .
.
(1)求 的定义域;
的定义域;
(2)判断 的奇偶性;
的奇偶性;
(3)判断 单调性并用定义证明.
单调性并用定义证明.
16、(满分12分)
已知A={1,2,x2-5x+9},B={3,x2+ax+a},如果A={1,2,3},2 ∈B,
求实数a的值.
15、12.若对任意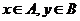 ,(
,(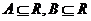 )有唯一确定的
)有唯一确定的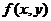 与之对应,则称
与之对应,则称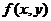 为关于
为关于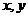 的二元函数。
的二元函数。
定义:满足下列性质的二元函数 为关于实数
为关于实数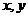 的广义“函数”:
的广义“函数”:
(1)非负性: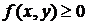 ,当且仅当
,当且仅当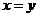 时取等号;
时取等号;
(2)对称性: ;
;
(3)三角形不等式: 对任意的实数
对任意的实数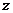 均成立.
均成立.
给出三个二元函数:①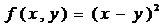 ;②
;②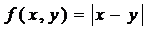 ; ③
; ③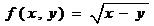 .④
.④
请选出所有能够成为关于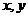 的广义“函数”的序号_______________.
的广义“函数”的序号_______________.
14、函数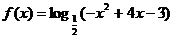 的递减区间为________
的递减区间为________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com