
2.了解互斥事件、对立事件的意义及其运算公式.
1.了解随机事件发生的不确定性和频率的稳定性,了解概率的意义,了解频率与概率的区别。
20. (1)当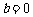 时,
时, ,
,
若 ,
, ,则
,则 在
在 上单调递减,符合题意;
上单调递减,符合题意;
若 ,要使
,要使 在
在 上单调递减,
上单调递减,
必须满足 ∴
∴ .综上所述,a的取值范围是
.综上所述,a的取值范围是 .
.
(2)若 ,
, ,则
,则 无最大值,
无最大值,
故 ,∴
,∴ 为二次函数,
为二次函数,
要使 有最大值,必须满足
有最大值,必须满足 即
即 且
且 ,
,
此时, 时,
时, 有最大值.
有最大值.
又 取最小值时,
取最小值时, ,
,
依题意,有 ,则
,则 ,
,
∵ 且
且 ,∴
,∴ ,得
,得 ,此时
,此时 或
或 .
.
∴满足条件的整数对 是
是 .
.
(3)当整数对是 时,
时,
 ,
, 是以2为周期的周期函数,
是以2为周期的周期函数,
又当 时,
时, ,构造
,构造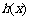 如下:当
如下:当 ,则,
,则,
 ,
,
故
19. 解(1)
①当 时,
时, 上为增函数
上为增函数
故 ②
②
当 上为减函数
上为减函数
故
(2) 即
即


即
18. 
 ,所以
,所以
因为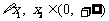 时,恒有
时,恒有 ,所以
,所以
经过计算得: =-3,
=-3,
 ,
,
所以 ,解得:
,解得: .
.
17.(1) ,
, ,
, ,所以
,所以
 ,
, 不是奇函数;
不是奇函数;
(2) 是奇函数时,
是奇函数时, ,即
,即 对任意实数
对任意实数 成立.
成立.
化简整理得 ,这是关于
,这是关于 的恒等式,所以
的恒等式,所以
 所以
所以 (舍)或
(舍)或 .
.
(3)(理) ,因为
,因为 ,所以
,所以 ,
, ,从而
,从而 ;
;
而 对任何实数
对任何实数 成立;
成立;
所以对任何实数 、c都有
、c都有 成立.
成立.
(文)  ,因为
,因为 ,
,
所以 ,
, ,
,
从而 ;所以函数
;所以函数 的值域为
的值域为 .
.
16. [解] (1) ,
, ,
, ,
,
 (
( ),
), (
( )(两个函数各3分)
)(两个函数各3分)
(2)设:投资债券类产品 万元,则股票类投资为
万元,则股票类投资为 万元
万元


令 ,则
,则 =
= =
=
所以当 ,即
,即 万元时,收益最大,
万元时,收益最大, 万元.
万元.
15. (1) ; (2)
; (2) .
.
14.函数 在
在 -∞,+∞
-∞,+∞ 上单调递增(或
上单调递增(或 =
= +
+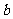 (
( >0)等)
>0)等)
10.330 11. 3
12.  13.
13. 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com