
7.月球的质量约为7.35×1022kg,绕地球运行的轨道半径是3.84×105km,运行的周期是27.3天,则月球受到地球所施的向心力的大小是_____。2.33×1020
6.宇宙间的一切物体都是互相极引的,两个物体间的引力大小,跟它们的 成正比,跟它们的 成反比,这就是万有引力定律.万有引力恒量G=6.67×10-11 .第一个比较精确测定这个恒量的是英国物理学家 .
质量的乘积,距离的二次方, Nm2/kg2 ,卡文迪许
5.设想把一质量为m的物体放在地球的中心,这时它受到地球对它的万有引力是(A )
A. 0 B. mg (g=9.8m/s2) C.∞ D.无法确定
4.地球质量大约是月球质量的81倍,在登月飞船通过月、地之间的某一位置时,月球和地球对它的引力大小相等,该位置到月球中心和地球中心的距离之比为(B )
A.1:27 B. 1:9 C. 1:3 D. 9:1
3.设地球表面物体的重力加速度为g0,某卫星在距离地心3R(R是地球的半径)的轨道上绕地球运行,则卫星的加速度为(B )
A.g0 B.g0/9 C.g0/4 D.g0/16
2.下列关于陨石坠向地球的解释中,正确的是(B )
A.陨石对地球的吸引力远小于地球对陨石的吸引力
B.陨石对地球的吸引力和地球对陨石的吸引力大小相等,但陨石的质量小,加速度大,所以改变运动方向落向地面
C.太阳不再吸引陨石,所以陨石落向地球
D.陨石受到其它星球的斥力而落向地球
1.对于万有引力定律的表述式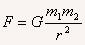 ,下面说法中正确的是(AD)
,下面说法中正确的是(AD)
A.公式中G为引力常量,它是由实验测得的,而不是人为规定的
B.当r趋近于零时,万有引力趋于无穷大
C. m1与m2受到的引力大小总是相等的,方向相反,是一对平衡力
D. m1与m2受到的引力总是大小相等的,而与m1、m2是否相等无关
4.卡文迪许扭秤实验证明了万有引力的存在及正确性,并使得万有引力定律可以定量计算,推动了天文学的发展。充分体现了实验对物理学发展的意义。说明了实践是检验真理的唯一标准。
[范例精析]
例1:氢原子有一个质子和围绕质子运动的电子组成,已知质子的质量为1.67×10-27kg,电子的质量为9.1×10-31kg,如果质子与电子的距离为1.0×10-10m,求它们之间的万有引力。
解析:本题由于质子和电子的尺寸大小远小于它们间的距离,可以将它们看作质点,运用万有引力定律直接求解。
根据万有引力定律质子与电子之间的万有引力为
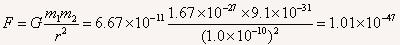 N
N
答:电子与质子之间的万有引力大小为1.01×10-47N。
拓展:应用万有引力定律计算物体间的万有引力时,应该注意万有引力定律的适用条件。万有引力定律适用于计算两个质点间的万有引力,对于质量均匀分布的球体,仍可以用万有引力定律,公式中的r为球心之间的距离。另外当两个物体间的距离比它们自身的尺寸大得多的时候,可以把两个物体当作质点,应用万有引力定律进行计算。
例2:设地球表面物体的重力加速度为g0,物体在距离地心4R(R是地球的半径)处,由于地球的作用而产生的加速度为g,则g/g0为( )
A.1 B.1/9 C.1/4 D.1/16
解析:本题是万有引力定律的简单应用,物体在地球表面的重力加速度和在高空中的加速度都是由地球对物体的万有引力产生的。根据万有引力定律和牛顿第二定律就可以解决该题。
设地球质量为M,质量为m的物体受到地球的万有引力产生加速度,在地球表面和高空分别有:
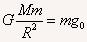
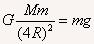
解得:g/g0=1/16
答案选:D
拓展:物体运动的加速度由它受到的力产生,通常情况下不考虑地球的自转,物体受到的重力大小就认为等于它受到地球的万有引力。本题中物体在地面的重力加速度和高空中运动的加速度都认为是万有引力产生的,然后运用牛顿第二定律,建立物体受到的万有引力与物体运动的加速度之间的联系,从而解决问题。
例3:卡文迪许测出万有引力常量后,人们就能计算出地球的质量。现公认的引力常量G=6.67×10-11Nm2/kg2,请你利用引力常量、地球半径R和地面重力加速度g,估算地球的质量。(R=6371km,g=9.8m/s2)
解析:应用万有引力定律计算地球质量,需要知道物体和地球间的万有引力,本题中可以认为引力等于重力,用重力加速度表示引力。
根据万有引力定律
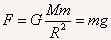 ,
,
得: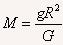 =5.967×1024kg
=5.967×1024kg
答:地球得质量为5.967×1024kg。
拓展:在应用万有引力定律解决有关地面上物体和地球的问题时,通常可以将重力和万有引力相替代。
[能力训练]
3.万有引力定律的内容是:自然界中任何两个物体都相互吸引,引力的大小与物体的质量m1和m2的乘积成正比,与它们之间距离r的二次方成反比。其数学表达式是_______________。万有引力定律的发现,证明了天体运动和地面上运动遵守共同的力学原理,实现了天地间力学的大综合,第一次揭示了自然界中的一种基本相互作用规律。这是人类认识历史上的一个重大飞跃。万有引力在天体运动中起着主要作用,在宇宙探索研究中有很重要的应用。
万有引力定律适用于计算两个质点间的万有引力,对于质量均匀分布的球体,仍可以用万有引力定律,公式中的r为球心之间的距离。另外当两个物体间的距离比它们自身的尺寸大得多的时候,可以把两个物体当作质点,应用万有引力定律进行计算。当研究物体不能看成质点时,可把物体假想分割成无数个质点,求出一个物体上每个质点与另一物体上每一个质点的万有引力然后求合力。
2.“月-地检验”将月球的向心加速度与地面附近的重力加速度进行比较,证明了地球对它表面附近物体的引力与地球对月球的引力以及太阳和行星间的引力符合同样的规律,是同一种力。“月-地检验”的过程,应用了“猜想假设-实验(事实)验证”的科学思想方法。
“月-地检验”基本思路是:月球到地心的距离是地面上物体到地心距离(地球半径)的60倍,如果月球受到地球的引力与地面上物体受到的力是同一种力,也就是引力的大小与距离的二次方成反比,那么月球的向心加速度应该是地面上物体重力加速度的1/602。牛顿通过计算,证实了他的假想,进而提出了万有引力定律。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com