
5.一艘宇宙飞船在一个星球表面附近作圆形轨道环绕飞行,宇航员要估测该星球的密度,只需要(C)
A.测定飞船的环绕半径
B.测定行星的质量
C.测定飞船的环绕周期
D.测定飞船的环绕速度
4.为了计算地球的质量必须知道一些数据,下列各组数据加上已知的万有引力常量为G,可以计算地球质量的是(BC)
A.地球绕太阳运行的周期T和地球离太阳中心的距离R
B.月球绕地球运行的周期T和月球离地球中心的距离R
C.人造地球卫星在地面附近运行的速度v和运行周期T
D.地球自转周期T和地球的平均密度ρ
3.由于地球自转,又由于地球的极半径较短而赤道半径较长,使得在地球表面的同一物体受到的重力(A)
A.在两极较大 B.在赤道较大
C.在两极跟在赤道一样大 D.无法判断
2.离地面高度h处的重力加速度是地球表面重力加速度的1/2,则高度是地球半径的(D)
A. 2倍 B.1/2倍 C. 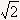 倍 D.(
倍 D.(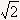 -1)倍
-1)倍
1.人造地球卫星A和B,它们的质量之比为mA:mB=1:2,它们的轨道半径之比为2:1,则下面的结论中正确的是(BC).
A.它们受到地球的引力之比为FA:FB=1:1
B.它们的运行速度大小之比为vA:vB=1: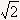
C.它们的运行周期之比为TA:TB=2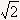 :1
:1
D.它们的运行角速度之比为ωA:ωB=3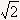 :1
:1
2.发现未知天体等:问题的发现:天文学家在用牛顿的引力理论分析天王星运动时,发现用万有引力定律计算出来的天王星的轨道与实际观测到的结果不相符,发生了偏离。两种观点:一是万有引力定律不准确;二是万有引力定律没有问题,只是天王星轨道外有未知的行星吸引天王星,使其轨道发生偏离。亚当斯和勒维耶的计算及预言:亚当斯和勒维耶相信未知行星的存在(即第二种假设)。他们根据天王星的观测资料,各自独立地利用万有引力定律计算出这颗“新”行星的轨道。伽勒的发现:1846年,德国科学家伽勒在勒维耶预言的位置附近发现了海王星。和预言的位置只差1度。在理论指导下进行有目的的观察,用观察到的事实结果验证了万有引力定律的准确性。1930年,汤姆根据洛韦尔对海王星轨道异常的分析,发现了冥王星。未知天体的发现是根据已知天体的轨道偏离,由万有引力定律推测并计算未知天体的轨道并预言它的位置从而发现未知天体。
[范例精析]
例1:地球和月球的中心距离大约是r=4×108m,试估算地球的质量。估算结果要求保留一位有效数字。
解析:月球是绕地球做匀速运动的天体,它运动的向心力由地球对它的引力提供。根据牛顿定律和万有引力定律,可以列式求出地球质量。月球绕地球运动的周期约为27.3天,由于本题是估算,且只要求结果保留一位有效数字,可以取月球周期T=30天。
设地球质量为M,月球质量为m,有
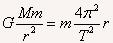
得到地球质量
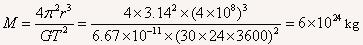
拓展:本题主要是依据课本计算太阳质量的思路和方法进行计算,从中体会解题思路和方法。由于有关天体的数据计算比较复杂,要注意细心、准确,提高自己的估算能力。
例2:已知地球半径R约为6.4×106m,地球质量M约为6×1024kg,引力常量G为6.67×10-11Nm2/kg2,近地人造地球卫星的周期T近约为85min,估算月球到地心的距离。
解析:本题的研究对象为月球,可以认为它绕地球做匀速圆周运动,圆周运动的向心力由地球对它的引力提供。本题还可以用到一个常识,即月球的周期T为一个月,约为30天。
解法一:对月球,万有引力提供向心力,有
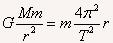 (m为月球质量)
(m为月球质量)
得: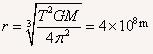
答:月球到地心的距离为4×108m。
解法二:对月球有
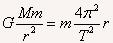
设地面上有一物体质量为m’,在不考虑地球自转时有
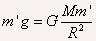 ,得
,得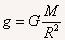 ,
,
代入上式得到
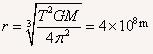
答:月球到地心的距离为4×108m。
解法三:利用开普勒第三定律求解:
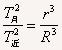
得: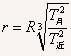
=4×108m
答:月球到地心的距离为4×108m。
拓展:本题方法一和方法二,仍然依据“将天体运动看成圆周运动,天体和中心天体间得万有引力提供向心力”的思路解题。方法一利用地球质量和引力常量,方法二运用地球表面物体的重力近似等于引力,作了替换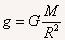 。这种方法常常会被采用。方法三则运用开普勒第三定律解决勒问题。学习中要开阔思路,多练习从不同角度去思考问题。
。这种方法常常会被采用。方法三则运用开普勒第三定律解决勒问题。学习中要开阔思路,多练习从不同角度去思考问题。
例3:两个星球组成双星,它们在相互之间的万有引力作用下,绕连线上某点做周期相同的匀速圆周运动。现测得两星中心距离为R,其运动周期为T,求两星的总质量。
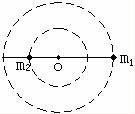
解析:双星之间的相互引力提供它们做匀速圆周运动的向心力,由于向心力总指向圆心,所以圆心在两星的连线上,且它们的角速度相同。如图所示,虚线圆是它们的轨道。
设它们的质量分别是m1、m2,两星到圆心的距离分别是L1、L2,做圆周运动的周期为T,根据万有引力提供向心力,有
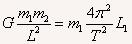
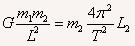
由于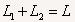
解得: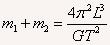
拓展:对于这种问题,不仅要明确万有引力提供向心力,还要注意到天体运动的特点和空间位置分布,特别要注意,万有引力中的距离L和两星做圆周运动的半径L1、L2之间的区别。另外要明确两星运动之间的联系,即向心力、周期相同。
[要点导学]
1.计算天体质量(或密度)。应用万有引力定律计算天体质量的基本思路和方法是将围绕某天体的行星的运动看成圆周运动,根据行星运动的向心力由它们间的万有引力提供建立方程,求出天体质量(或密度)。
(1)在不考虑地球自转的影响时,地面上物体受到的引力大小等于物体的重力。利用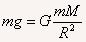 。解得地球质量_________。卡文迪许用扭秤测量了铅球间得作用力大小,得到了引力常量G,进而计算了地球的质量。从而使得万有引力定律进入定量计算领域,有了更实用的意义。
。解得地球质量_________。卡文迪许用扭秤测量了铅球间得作用力大小,得到了引力常量G,进而计算了地球的质量。从而使得万有引力定律进入定量计算领域,有了更实用的意义。
(2)根据卡文迪许计算地球质量的思路,我们还可以计算天体表面的重力加速度,某行星表面物体受到行星的引力大小等于物体在该行星表面的重力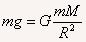 ,解得:
,解得: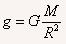 。式中M为行星质量,R为行星半径
。式中M为行星质量,R为行星半径
(3)行星绕太阳做匀速圆周运动的向心力是由它们之间的万有引力提供的,由此可以列出方程,从中解出太阳的质量。
(4)假如一个近地卫星(离地高度忽略,运动半径等于地球半径R)的运行周期是T。有: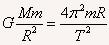 ,解得地球质量为___________;由于地球的体积为
,解得地球质量为___________;由于地球的体积为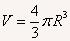 可以计算地球的密度为:______________.
可以计算地球的密度为:______________.
10.某行星自转一周所需时间为地球上的6小时。若该行星能看作球体,它的平均密度为3.03×103kg /m3。已知万有引力恒量G=6.67×10-11N·m2/kg2,在这行星上两极时测得一个物体的重力是10N。则在该行星赤道上称得物重是多少?9.5N
9.某星球的质量约为地球质量的9倍,半径约为地球的一半。若从地球上高h处平抛一物体,射程为15m,则在该星球上从同样的高度,以同样的初速度平抛该物体,其射程为多少?2.5m
8.地球是一个不规则的椭球,它的极半径为6357km,赤道半径为6378km,已知地球质量M=5.98×1024kg。不考虑地球自转的影响,则在赤道、极地用弹簧秤测量一个质量为1kg的物体,示数分别为多少?9.87N , 9.81N
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com