
3.下面加点字,解释为动词“说话”或“说”的意思的一项是
①王笑而不言②具以沛公言报项王③讽《诗》、《书》百家之言④佚之狐言于郑伯曰⑤而侯生曾无一言半辞送我⑥广故数言欲亡⑦凡六百一十二言,命曰《琵琶行》
A.①②③④ B.②⑤⑥ C.①④⑥ D.①②④⑥
2.下列各句中“请”字用法相同的是
①请往谓项伯,言沛公不敢背项王也②郡之贤士大夫请于当道③可以一战,战则请从④王好战,请以战喻⑤军中无以为乐,请以剑舞⑥其后用兵,则遣从事以少牢告庙,请其矢
A.①②③④⑤ B.①③④⑤ C.①②③⑤⑥ D.①②③⑥
1.下列各句对“兴”的解释,不正确的一项是
A.稽其成败兴坏之纪 (高兴) B.抑王兴甲兵,危士臣…… (发动)
C.积土成山,风雨兴焉 (产生) D.每览此人兴戚之由 (发生)
E.兴尽悲来 (兴致)
4.设α、β是关于方程 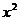 -2(k -1)x+k+1=0的两个实根,求 y=
-2(k -1)x+k+1=0的两个实根,求 y=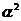 +
+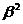 关于k的解析式,并求y的取值范围
关于k的解析式,并求y的取值范围
(y=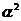 +
+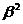 =4(k-
=4(k-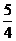 )2 -
)2 -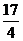 , k≥3或k≤0, 得y≥2.)
, k≥3或k≤0, 得y≥2.)
3.对于任意实数x,代数式 (5-4a-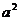 )
)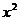 -2(a-1)x-3的值恒为负值,求a的取值范围(a≥1或a<-8)
-2(a-1)x-3的值恒为负值,求a的取值范围(a≥1或a<-8)
2.如果对于任何实数x,不等式kx2-kx+1>0 (k>0)都成立,那么k的取值范围是 (0<k<4)
1.如果不等式x2-2ax+1≥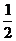 (x-1)2对一切实数x都成立,a的取值范围是
(0≤a≤1)
(x-1)2对一切实数x都成立,a的取值范围是
(0≤a≤1)
例1解关于x的不等式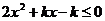
分析 此不等式为含参数k的不等式,当k值不同时相应的二次方程的判别式的值也不同,故应先从讨论判别式入手.
解 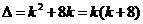
(1) 当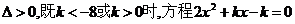 有两个不相等的实根.
有两个不相等的实根.
所以不等式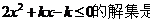 :
:
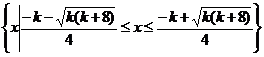
(2) 当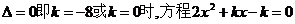 有两个相等的实根,
有两个相等的实根,
所以不等式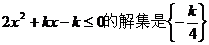 ,即
,即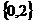 ;
;
(3) 当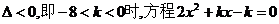 无实根
无实根
所以不等式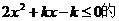 解集为
解集为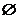 .
.
说明 一元二次方程、一元二次不等式、一元二次函数有着密切的联系,要注意数形结合研究问题.
小结:讨论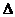 ,即讨论方程根的情况
,即讨论方程根的情况
例2.解关于x的不等式:(x-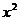 +12)(x+a)<0.
+12)(x+a)<0.
解:①将二次项系数化“+”为:(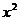 -x-12)(x+a)>0,
-x-12)(x+a)>0,
②相应方程的根为:-3,4,-a,现a的位置不定,应如何解?
③讨论:
ⅰ当-a>4,即a<-4时,各根在数轴上的分布及穿线如下:
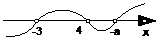 ∴原不等式的解集为{x| -3<x<4或x>-a}.
∴原不等式的解集为{x| -3<x<4或x>-a}.
ⅱ当-3<-a<4,即-4<a<3时,各根在数轴上的分布及穿线如下:
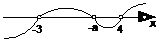 ∴原不等式的解集为{x| -3<x<-a或x>4}.
∴原不等式的解集为{x| -3<x<-a或x>4}.
ⅲ当-a<-3,即a>3时,各根在数轴上的分布及穿线如下:
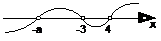 ∴原不等式的解集为{x| -a<x<-3或x>4}.
∴原不等式的解集为{x| -a<x<-3或x>4}.
ⅳ0当-a=4,即a=-4时,各根在数轴上的分布及穿线如下:
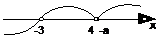 ∴原不等式的解集为{x| x>-3}.
∴原不等式的解集为{x| x>-3}.
ⅴ当-a=-3,即a=3时,各根在数轴上的分布及穿线如下:
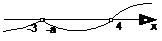 ∴原不等式的解集为{x| x>4}.
∴原不等式的解集为{x| x>4}.
小结:讨论方程根之间的大小情况
例3若不等式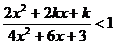 对于x取任何实数均成立,求k的取值范围.
对于x取任何实数均成立,求k的取值范围.
解:∵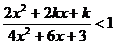
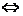
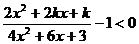
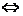
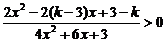
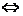
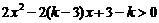 (∵4x2+6x+3恒正),
(∵4x2+6x+3恒正),
∴原不等式对x取任何实数均成立,等价于不等式2x2-2(k-3)x+3-k>0对x取任何实数均成立.
∴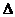 =[-2(k-3)]2-8(3-k)<0
=[-2(k-3)]2-8(3-k)<0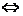 k2-4k+3<0
k2-4k+3<0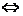 1<k<3.
1<k<3.
∴k的取值范围是(1,3).
小结:逆向思维题目,告诉解集反求参数范围,即确定原不等式,待定系数法的一部分
例4 已知关于x的二次不等式:a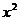 +(a-1)x+a-1<0的解集为R,求a的取值范围.
+(a-1)x+a-1<0的解集为R,求a的取值范围.
分析:原不等式的解集为R,即对一切实数x不等式都成立,故必然y= a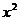 +(a-1)x+a-1的图象开口向下,且与x轴无交点,反映在数量关系上则有a<0 且
+(a-1)x+a-1的图象开口向下,且与x轴无交点,反映在数量关系上则有a<0 且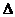 <0.
<0.
解:由题意知,要使原不等式的解集为R,必须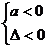 ,
,
即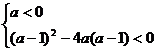
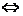
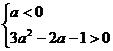
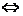
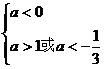
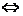 a<-
a<-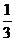 . ∴a的取值范围是a∈(-
. ∴a的取值范围是a∈(-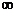 ,-
,-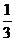 ).
).
说明:本题若无“二次不等式”的条件,还应考虑a=0的情况,但对本题讲a=0时式子不恒成立.(想想为什么?)
练习:已知(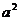 -1)
-1)
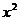 -(a-1)x-1<0的解集为R,求实数a的取值范围.
-(a-1)x-1<0的解集为R,求实数a的取值范围.
解:若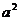 -1=0,即a=1或a=-1时,原不等式的解集为R和{x|x<
-1=0,即a=1或a=-1时,原不等式的解集为R和{x|x<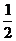 };
};
若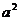 -1
-1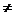 0,即a
0,即a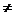
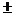 1时,要使原不等式的解集为R,
1时,要使原不等式的解集为R,
必须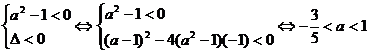 .
.
∴实数a的取值范围是(-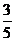 ,1)∪{1}=(-
,1)∪{1}=(-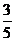 ,1).
,1).
2.一元一次、一元二次、高次、分式不等式得解法及注意事项
1.函数、方程、不等式的关系
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com